5  Randomized Complete Block Design

Randomized complete block design (RCBD) is very common design where experimental treatments are applied at random to experimental units within each block. The block can represent a spatial or temporal unit or even different technicians taking data. The blocks are intended to control for a nuisance source of variation, such as over time, spatial variance, changes in equipment or operators, or myriad other causes. They are a random effect where the actual blocks used in the study are a random sample of a distribution of other blocks.

5.1 Background

The statistical model:

\[y_{ij} = \mu + \alpha_i + \beta_j + \epsilon_{ij}\] Where:

\(\mu\) = overall experimental mean \(\alpha\) = treatment effects (fixed) \(\beta\) = block effects (random) \(\epsilon\) = error terms

\[ \epsilon \sim N(0, \sigma)\]

\[ \beta \sim N(0, \sigma_b)\]

Both the overall error and the block effects are assumed to be normally distributed with a mean of zero and standard deviations of \(\sigma\) and \(\sigma_B\), respectively.

5.2 Example Analysis

First, load the libraries for analysis and estimation:

library(lme4); library(lmerTest); library(emmeans)
library(dplyr); library(performance)
library(nlme); library(performance); library(emmeans)
library(dplyr)

This data set is for a single wheat variety trial conducted in Aberdeen, Idaho in 2015. The trial includes 4 blocks and 42 different treatments (wheat varieties in this case). This experiment consists of a series of plots (the experimental unit) laid out in a rectangular grid in a farm field. The goal of this analysis is the estimate the yield of each variety and the determine the relative rankings of the varieties.

var_trial <- read.csv(here::here("data", "aberdeen2015.csv"))
Table of variables in the data set
block blocking unit
range column position for each plot
row row position for each plot
variety crop variety (the treatment) being evaluated
yield_bu_a yield (bushels per acre)

5.2.1 Data integrity checks

The first thing is to make sure the data is what we expect.We will the steps explained in Chapter 4. Here are the steps to verify our data:

  • Check structure of the data
str(var_trial)
'data.frame':   168 obs. of  5 variables:
 $ block     : int  4 4 4 4 4 4 4 4 4 4 ...
 $ range     : int  1 1 1 1 1 1 1 1 1 1 ...
 $ row       : int  1 2 3 4 5 6 7 8 9 10 ...
 $ variety   : chr  "DAS004" "Kaseberg" "Bruneau" "OR2090473" ...
 $ yield_bu_a: num  128 130 119 115 141 ...

These look okay except for block, which is currently coded as integer (numeric). We don’t want run a regression of block, where block 2 has twice the effect of block 1, and so on. So, converting it to a character will fix that. It can also be converted to a factor, but character variables are a bit easier to work with, and ultimately, equivalent to factor conversion

var_trial$block <- as.character(var_trial$block)
  • Inspect the independent variables

Next, check the independent variables. Running a cross tabulations is often sufficient to ascertain this.

table(var_trial$variety, var_trial$block)
                        
                         1 2 3 4
  06-03303B              1 1 1 1
  Bobtail                1 1 1 1
  Brundage               1 1 1 1
  Bruneau                1 1 1 1
  DAS003                 1 1 1 1
  DAS004                 1 1 1 1
  Eltan                  1 1 1 1
  IDN-01-10704A          1 1 1 1
  IDN-02-29001A          1 1 1 1
  IDO1004                1 1 1 1
  IDO1005                1 1 1 1
  Jasper                 1 1 1 1
  Kaseberg               1 1 1 1
  LCS Artdeco            1 1 1 1
  LCS Biancor            1 1 1 1
  LCS Drive              1 1 1 1
  LOR-833                1 1 1 1
  LOR-913                1 1 1 1
  LOR-978                1 1 1 1
  Madsen                 1 1 1 1
  Madsen / Eltan (50/50) 1 1 1 1
  Mary                   1 1 1 1
  Norwest Duet           1 1 1 1
  Norwest Tandem         1 1 1 1
  OR2080637              1 1 1 1
  OR2080641              1 1 1 1
  OR2090473              1 1 1 1
  OR2100940              1 1 1 1
  Rosalyn                1 1 1 1
  Stephens               1 1 1 1
  SY  Ovation            1 1 1 1
  SY 107                 1 1 1 1
  SY Assure              1 1 1 1
  UI Castle CLP          1 1 1 1
  UI Magic CLP           1 1 1 1
  UI Palouse             1 1 1 1
  UI Sparrow             1 1 1 1
  UI-WSU Huffman         1 1 1 1
  WB 456                 1 1 1 1
  WB 528                 1 1 1 1
  WB1376 CLP             1 1 1 1
  WB1529                 1 1 1 1

There are 42 varieties and there appears to be no misspellings among them that might confuse R into thinking varieties are different when they are actually the same. R is sensitive to case and white space, which can make it easy to create near duplicate treatments, such as “eltan” and “Eltan”. There is no evidence of that in this data set. Additionally, it is perfectly balanced, with exactly one observation per treatment per rep. Please note that this does not tell us anything about the extent of missing data.

  • Check the extent of missing data

Here is a quick check to count the number of missing data in each column.

colSums(is.na(var_trial))
     block      range        row    variety yield_bu_a 
         0          0          0          0          0

Alas, no missing data.

  • Inspect the dependent variable

Last, check the dependent variable by creating a histogram.

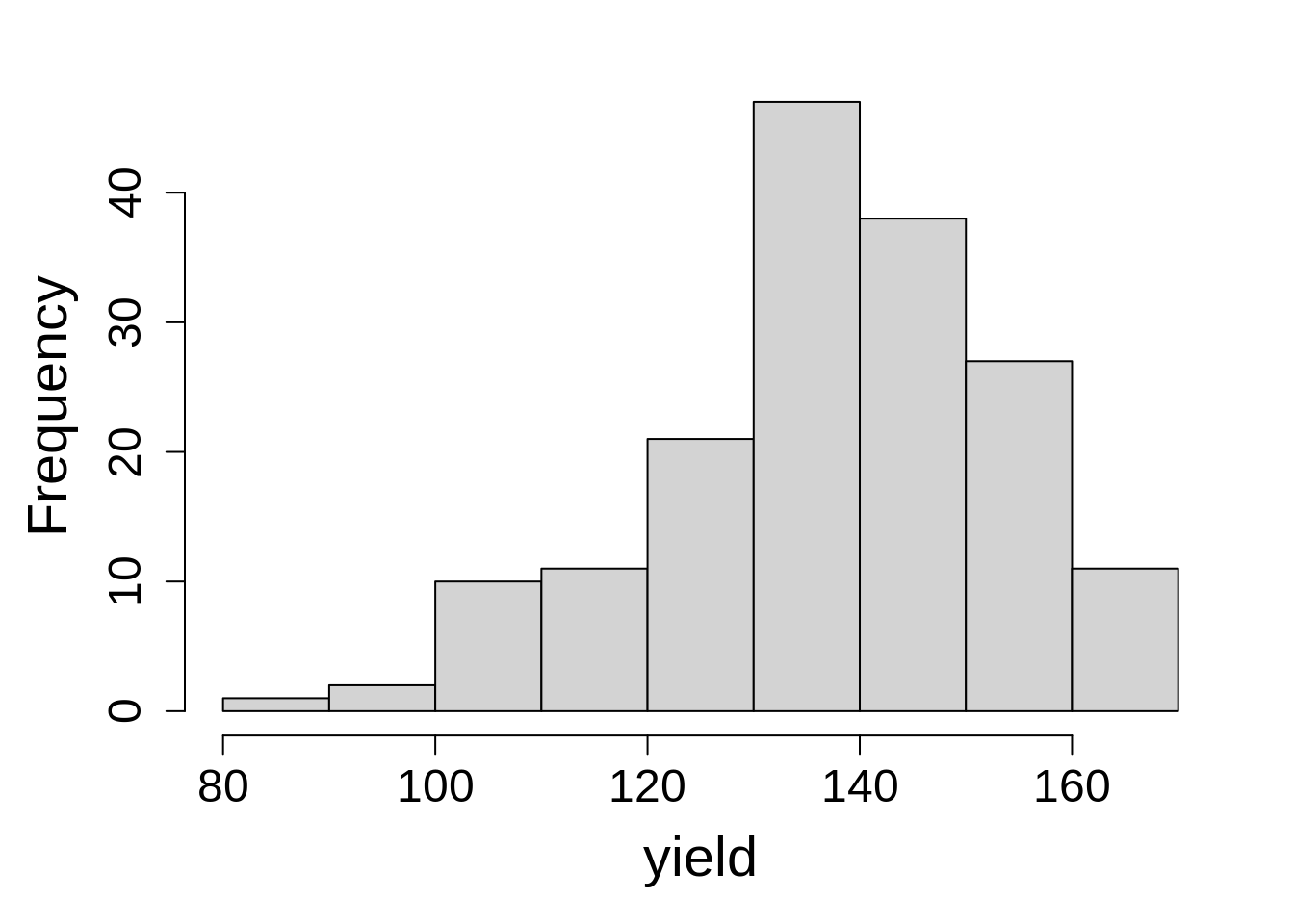
Figure 5.1: Histogram of the dependent variable. 
hist(var_trial$yield_bu_a, main = NA, xlab = "yield")

The range is roughly falling into the range we expect. We (the authors) know this from talking with the person who generated the data, not through our own intuition. There are no large spikes of points at a single value (indicating something odd), nor are there any extreme values (low or high) that might indicate problems.

This data set is ready for analysis!

5.2.2 Model Building

Recall the model:

\[y_{ij} = \mu + \alpha_i + \beta_j + \epsilon_{ij}\]

For this model, \(\alpha_i\) is the variety effect (fixed) and \(\beta_j\) is the block effect (random).

Here is the R syntax for the RCBD statistical model:

model_rcbd_lmer <- lmer(yield_bu_a ~ variety + (1|block),
                   data = var_trial, 
                   na.action = na.exclude)
model_rcbd_lme <- lme(yield_bu_a ~ variety,
                  random = ~ 1|block,
                  data = var_trial, 
                  na.action = na.exclude)

5.2.3 Check Model Assumptions

Note

R syntax for checking model assumptions is the same for lme4 and nlme.

Remember those iid assumptions? Let’s make sure we actually met them.

5.2.3.1 Original Method

We will start inspecting the model assumptions by for checking the homoscedasticity (constant variance) first using a plot() function in base R.

Figure 5.2: Plot of residuals versus fitted values 
plot(model_rcbd_lmer, resid(., scaled=TRUE) ~ fitted(.), 
     xlab = "fitted values", ylab = "studentized residuals")

We have observed a random and uniform distribution of points. This looks good!

As explained in Chapter 4 we will first extract residuals usingresid() and then generate a qq-plot and line.

Figure 5.3: QQ-plot of residuals 
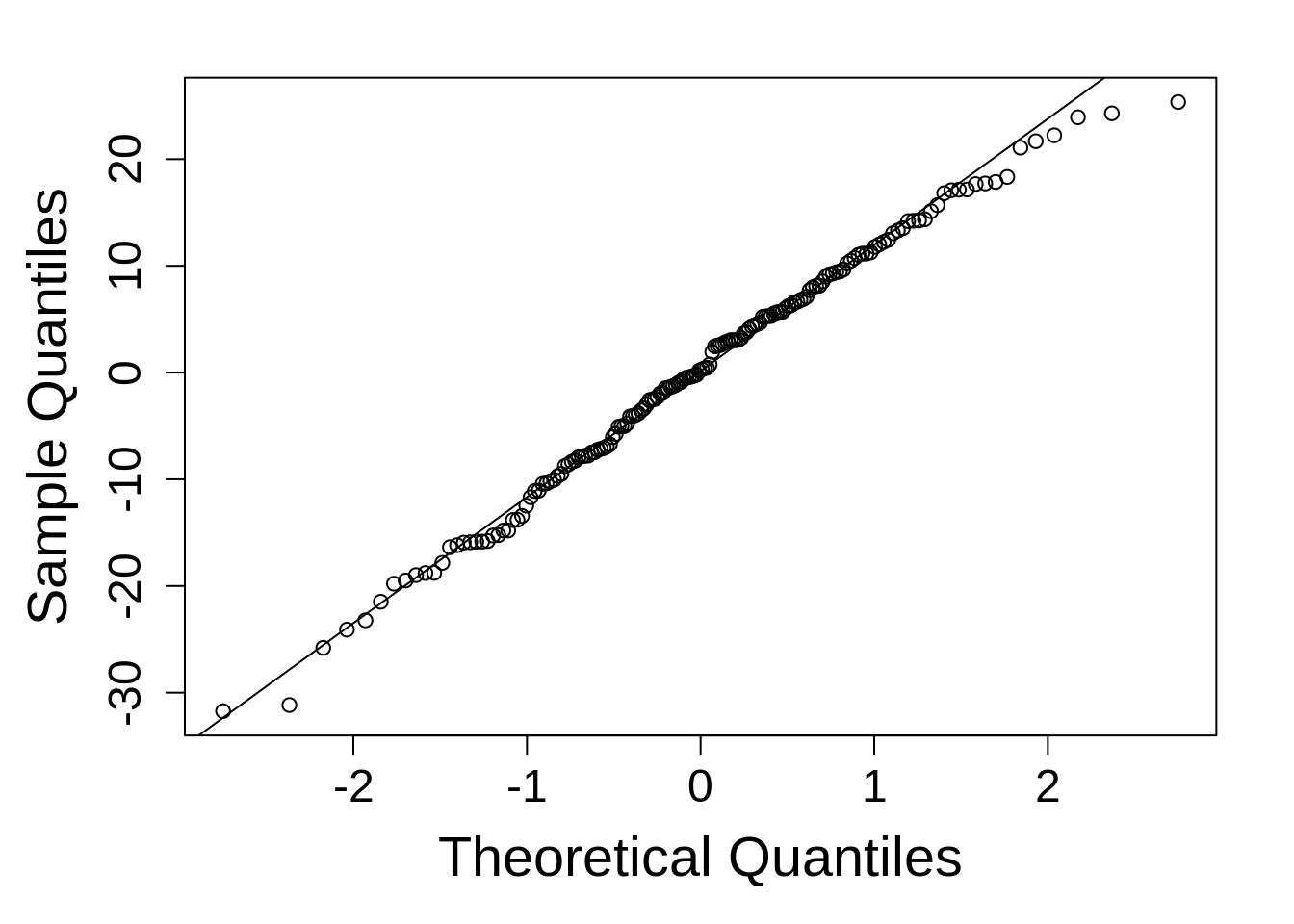
qqnorm(resid(model_rcbd_lmer), main = NULL); qqline(resid(model_rcbd_lmer))

This is reasonably good. Things do tend to fall apart at the tails a little, so this is not concerning.

5.2.3.2 New Method

Here, we will use the check_model() function from the performance package to look at the normality and linearity of the residuals.

check_model(model_rcbd_lmer,  check = c('qq', 'linearity', 'reqq'), detrend=FALSE, alpha = 0)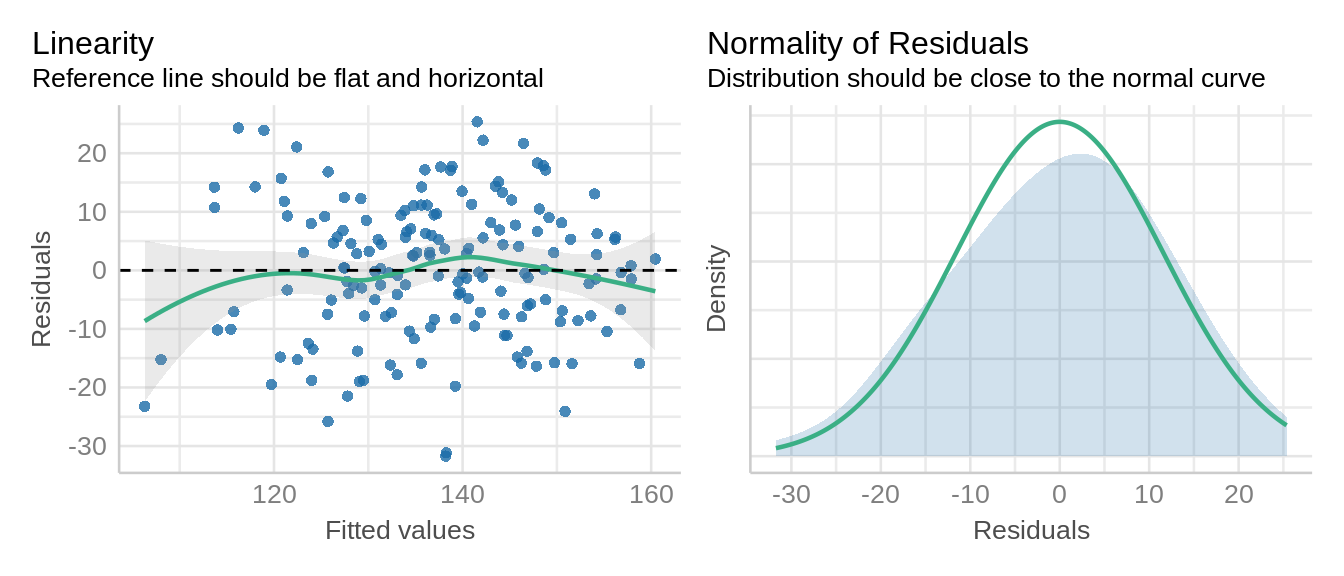

5.2.4 Inference

Note

R syntax for estimating model marginal means is the same for lme4 and nlme.

Estimates for each treatment level can be obtained with the emmeans package.

rcbd_emm <- emmeans(model_rcbd_lmer, ~ variety)
as.data.frame(rcbd_emm) %>% arrange(desc(emmean))
 variety                  emmean       SE    df  lower.CL upper.CL
 Rosalyn                155.2703 7.212203 77.85 140.91149 169.6292
 IDO1005                153.5919 7.212203 77.85 139.23310 167.9508
 OR2080641              152.6942 7.212203 77.85 138.33536 167.0530
 Bobtail                151.6403 7.212203 77.85 137.28149 165.9992
 UI Sparrow             151.6013 7.212203 77.85 137.24245 165.9601
 Kaseberg               150.9768 7.212203 77.85 136.61794 165.3356
 IDN-01-10704A          148.9861 7.212203 77.85 134.62729 163.3450
 06-03303B              148.8300 7.212203 77.85 134.47116 163.1888
 WB1529                 148.2445 7.212203 77.85 133.88568 162.6034
 DAS003                 145.2000 7.212203 77.85 130.84116 159.5588
 IDN-02-29001A          144.5755 7.212203 77.85 130.21665 158.9343
 Bruneau                143.9900 7.212203 77.85 129.63116 158.3488
 SY 107                 143.6387 7.212203 77.85 129.27987 157.9975
 WB 528                 142.9752 7.212203 77.85 128.61633 157.3340
 OR2080637              141.7652 7.212203 77.85 127.40633 156.1240
 Jasper                 141.2968 7.212203 77.85 126.93794 155.6556
 UI Magic CLP           139.5403 7.212203 77.85 125.18149 153.8992
 Madsen                 139.2671 7.212203 77.85 124.90826 153.6259
 LCS Biancor            139.1110 7.212203 77.85 124.75213 153.4698
 SY  Ovation            138.6426 7.212203 77.85 124.28375 153.0014
 OR2090473              137.8229 7.212203 77.85 123.46407 152.1817
 Madsen / Eltan (50/50) 136.9642 7.212203 77.85 122.60536 151.3230
 UI-WSU Huffman         135.4810 7.212203 77.85 121.12213 149.8398
 Mary                   134.8564 7.212203 77.85 120.49762 149.2153
 Norwest Tandem         134.3490 7.212203 77.85 119.99020 148.7079
 Brundage               134.0758 7.212203 77.85 119.71697 148.4346
 IDO1004                132.5145 7.212203 77.85 118.15568 146.8733
 DAS004                 132.2413 7.212203 77.85 117.88245 146.6001
 Norwest Duet           132.0852 7.212203 77.85 117.72633 146.4440
 Eltan                  131.4606 7.212203 77.85 117.10181 145.8195
 LCS Artdeco            130.8361 7.212203 77.85 116.47729 145.1950
 UI Palouse             130.4848 7.212203 77.85 116.12600 144.8437
 LOR-978                130.4458 7.212203 77.85 116.08697 144.8046
 LCS Drive              128.7674 7.212203 77.85 114.40858 143.1262
 Stephens               127.1671 7.212203 77.85 112.80826 141.5259
 OR2100940              126.1523 7.212203 77.85 111.79342 140.5111
 UI Castle CLP          125.5277 7.212203 77.85 111.16891 139.8866
 WB1376 CLP             123.6932 7.212203 77.85 109.33439 138.0521
 LOR-833                122.7565 7.212203 77.85 108.39762 137.1153
 LOR-913                118.7752 7.212203 77.85 104.41633 133.1340
 WB 456                 118.4629 7.212203 77.85 104.10407 132.8217
 SY Assure              111.0468 7.212203 77.85  96.68794 125.4056

Degrees-of-freedom method: kenward-roger 
Confidence level used: 0.95

This table indicates the estimated marginal means (“emmeans”, sometimes called “least squares means”), the standard error (“SE”) of those means, the degrees of freedom and the upper and lower bounds of the 95% confidence interval. As an additional step, the emmeans were sorted from largest to smallest.

At this point, the analysis goals have been met: we know the estimated means for each treatment and their rankings.

If you want to run ANOVA, it can be done quite easily. By default, sequential (type I) sums of squares is used by nlme, but partial (type 3) sums of squares is also possible. Containment is the only degrees of freedom calculation method enabled in nlme. The lmer-extender package **lmerTest* implements type 3 tests and the Kenward-Rogers method of degrees of freedom approximation by default.1

1 The Type I method is called “sequential” sum of squares because it adds terms to the model one at a time; while type 3 (“partial”) drops model terms one at a time. This can effect the results of an F-test and p-value, but only when a data set is unbalanced across treatments, either due to design or missing data points.

In this example, there is only one fixed effect (and the experiment is perfectly balanced), so the sums of squares choice is immaterial.

anova(model_rcbd_lmer, type = "1")
Type I Analysis of Variance Table with Satterthwaite's method
        Sum Sq Mean Sq NumDF DenDF F value    Pr(>F)    
variety  18354  447.65    41   123  2.4528 8.017e-05 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
anova(model_rcbd_lme, type = "sequential")
            numDF denDF   F-value p-value
(Intercept)     1   123 2514.1283  <.0001
variety        41   123    2.4528   1e-04