10  Incomplete Block Design

10.1 Background

The block design described in Chapter 4 was complete, meaning that each block contained each treatment level at least once. In practice, it may not be possible or advisable to include all treatments in each block, either due to limitations in treatment availability (e.g. limited seed stocks) or the block size becomes too large to serve its original goals of controlling for spatial variation.

In such cases, incomplete block designs (IBD) can be used. Incomplete block designs break the experiment into many smaller incomplete blocks that are nested within standard RCBD-style blocks and assigns a subset of the treatment levels to each incomplete block. There are several different approaches (Yates 1936) for how to assign treatment levels to incomplete blocks and these designs impact the final statistical analysis (and if all treatments included in the experimental design are estimable). An excellent description of incomplete block designs is provided by Lukas Meier in ANOVA and Mixed Models (2022) and his lecture notes as well as in lecture notes by Jennifer Kling.

Incomplete block designs are grouped into two groups: (1) balanced designs; and (2) partially balanced (also commonly called alpha-lattice) designs (Oehlert 2000). Balanced IBD designs have been previously called “lattice designs” (Nair 1952), but we are not using that term to avoid confusion with alpha-lattice designs. In a balanced design, treatment pairs occur together in equal numbers for all possible pairwise treatment combinations. This enables a user to conduct all pairwise comparisons, but it not always feasible to implement, particularly when there is a large number of treatment, such as in a crop variety trial. The balanced incomplete block designs are guided by strict principles and guidelines including: the number of treatments must be a perfect square (e.g. 25, 36, and so on), and number of replicates must be equal to number of blocks + 1.

In a partially balanced design, treatment pairs occur unequally across the experiments and some pairs do not occur at all. These designs are sometimes labelled “disconnected” when all treatment pairs do not occur together because those pairwise combinations can be contrasted in a statistical analysis. In alpha-lattice design, the sub-blocks are grouped into complete replicates. The replication is considered the “superblock” consisting of multiple sub-blocks and each treatment occurs at least once. These designs are also termed as “resolvable incomplete block designs” (Patterson and Williams 1976). This design has been more commonly used instead of balanced IBD because of it’s practicability and versatility when there is a large number of treatments. In this design, we have t treatment groups, each occurring r times, with bk experimental units groups into b blocks of size k<v in such a manner that units within a block are same and units in different blocks are substantially different.

10.1.1 Statistical Model

The statistical model for a balanced incomplete block design is:

\[y_{ij} = \mu + \alpha_i + \beta_j + \epsilon_{ij}\]

Where:

\(\mu\) = overall experimental mean
\(\alpha\) = treatment effects (fixed)
\(\beta\) = block effects (random)
\(\epsilon\) = error terms

\[ \epsilon \sim N(0, \sigma)\]

\[ \beta \sim N(0, \sigma_b)\]

There are few key points that we need to keep in mind when incomplete block experiments:

• Block can be treated as fixed (“intra-block analysis”) or random (“inter-block analysis”). When it is treated as random, the block effect also contains treatment effects.
• A drawback of this design is that the estimates have less precision compared to RCBD
• The very nature of incomplete block design results in ‘missing’ data from the standpoint of statistical software, thus ensuring that type I and type III sums of squares are different even there is no data missing for any experimental unit in the original design.
• Contrasting treatments within blocks can remove block effects, so it helps to ensure a design contains the pairwise treatment combinations of interest to the researcher.

10.2 Examples Analyses

10.2.1 Balanced Incomplete Block Design

We will demonstrate how to analyze an example balanced incomplete block design. First, load the libraries required for analysis.

lme4

library(lme4); library(lmerTest); library(emmeans)
library(dplyr); library(broom.mixed); library(performance)

nlme

library(nlme); library(broom.mixed); library(emmeans)
library(dplyr); library(performance)

The data used for this example analysis is from the agridat package (data set “weiss.incblock”). This example is comprised of soybean balanced incomplete block experiment.

weiss <- read.csv(here::here("data", "weiss_ICB.csv"))

Table of variables in the data set

block	blocking unit
gen	genotype (variety) factor
row	row position for each plot
col	column position for each plot
yield	grain yield in bu/ac

10.2.1.1 Data integrity checks

• Check structure of the data

We will start inspecting the data set first by looking at the class of each variable:

str(weiss)

'data.frame':   186 obs. of  5 variables:
 $ block: chr  "B01" "B02" "B03" "B04" ...
 $ gen  : chr  "G24" "G15" "G20" "G18" ...
 $ yield: num  29.8 24.2 30.5 20 35.2 25 23.6 23.6 29.3 25.5 ...
 $ row  : int  42 36 30 24 18 12 6 42 36 30 ...
 $ col  : int  1 1 1 1 1 1 1 2 2 2 ...

The variables we need for the model are block, gen, and yield. The block and gen are classified as factor variables and yield is numeric. Therefore, we do not need to change class of any of the required variables.

• Inspect the independent variables

Next, let’s check the independent variables. We can look at this by running a cross tabulations among block and gen factors.

agg_tbl <- weiss %>% group_by(gen) %>% 
  summarise(total_count=n(),
            .groups = 'drop')
agg_tbl

# A tibble: 31 × 2
   gen   total_count
   <chr>       <int>
 1 G01             6
 2 G02             6
 3 G03             6
 4 G04             6
 5 G05             6
 6 G06             6
 7 G07             6
 8 G08             6
 9 G09             6
10 G10             6
# ℹ 21 more rows

agg_df <- aggregate(weiss$gen, by=list(weiss$block), FUN=length)
agg_df

   Group.1 x
1      B01 6
2      B02 6
3      B03 6
4      B04 6
5      B05 6
6      B06 6
7      B07 6
8      B08 6
9      B09 6
10     B10 6
11     B11 6
12     B12 6
13     B13 6
14     B14 6
15     B15 6
16     B16 6
17     B17 6
18     B18 6
19     B19 6
20     B20 6
21     B21 6
22     B22 6
23     B23 6
24     B24 6
25     B25 6
26     B26 6
27     B27 6
28     B28 6
29     B29 6
30     B30 6
31     B31 6

There are 31 varieties and it is perfectly balanced, with exactly one observation per treatment per superblock.

• Check the extent of missing data

We can calculate the sum of missing values in variables in this data set to evaluate the extent of missing values in different variables:

colSums(is.na(weiss))

block   gen yield   row   col 
    0     0     0     0     0 

No missing data!

• Inspect the dependent variable

Last, let’s plot a histogram of the dependent variable. This is a quick check before analysis to see if there is any strong deviation in values.

Figure 10.1: Histogram of the dependent variable.

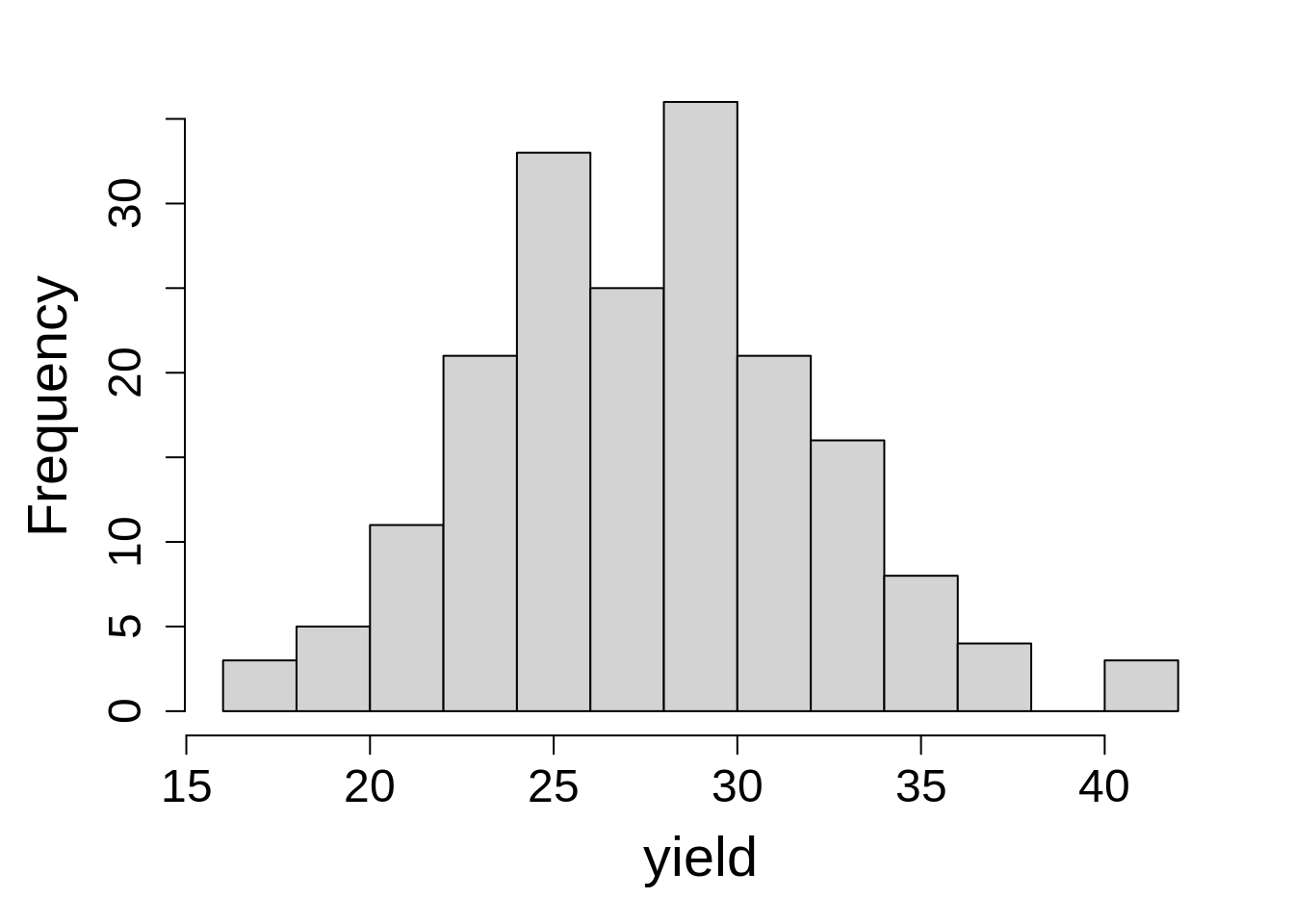
hist(weiss$yield, main = NA, xlab = "yield")

Response variable values fall within expected range, with few extreme values on right tail. This data set is ready for analysis!

10.2.1.2 Model Building

We will be evaluating the response of yield as affected by gen (fixed effect) and block (random effect/intra-block analysis).

lme4

model_icbd <- lmer(yield ~ gen + (1|block),
                   data = weiss, 
                   na.action = na.exclude)
tidy(model_icbd)

# A tibble: 33 × 8
   effect group term        estimate std.error statistic    df  p.value
   <chr>  <chr> <chr>          <dbl>     <dbl>     <dbl> <dbl>    <dbl>
 1 fixed  <NA>  (Intercept)  24.6        0.922   26.7     153. 2.30e-59
 2 fixed  <NA>  genG02        2.40       1.17     2.06    129. 4.17e- 2
 3 fixed  <NA>  genG03        8.04       1.17     6.88    129. 2.31e-10
 4 fixed  <NA>  genG04        2.37       1.17     2.03    129. 4.42e- 2
 5 fixed  <NA>  genG05        1.60       1.17     1.37    129. 1.73e- 1
 6 fixed  <NA>  genG06        7.39       1.17     6.32    129. 3.82e- 9
 7 fixed  <NA>  genG07       -0.419      1.17    -0.359   129. 7.20e- 1
 8 fixed  <NA>  genG08        3.04       1.17     2.60    129. 1.04e- 2
 9 fixed  <NA>  genG09        4.84       1.17     4.14    129. 6.22e- 5
10 fixed  <NA>  genG10       -0.0429     1.17    -0.0367  129. 9.71e- 1
# ℹ 23 more rows

nlme

model_icbd1 <- lme(yield ~ gen,
                  random = ~ 1|block,
                  data = weiss, 
                  na.action = na.exclude)
tidy(model_icbd1)

# A tibble: 33 × 8
   effect group term        estimate std.error    df statistic  p.value
   <chr>  <chr> <chr>          <dbl>     <dbl> <dbl>     <dbl>    <dbl>
 1 fixed  <NA>  (Intercept)  24.6        0.922   125   26.7    2.10e-53
 2 fixed  <NA>  genG02        2.40       1.17    125    2.06   4.18e- 2
 3 fixed  <NA>  genG03        8.04       1.17    125    6.88   2.54e-10
 4 fixed  <NA>  genG04        2.37       1.17    125    2.03   4.43e- 2
 5 fixed  <NA>  genG05        1.60       1.17    125    1.37   1.73e- 1
 6 fixed  <NA>  genG06        7.39       1.17    125    6.32   4.11e- 9
 7 fixed  <NA>  genG07       -0.419      1.17    125   -0.359  7.20e- 1
 8 fixed  <NA>  genG08        3.04       1.17    125    2.60   1.04e- 2
 9 fixed  <NA>  genG09        4.84       1.17    125    4.14   6.33e- 5
10 fixed  <NA>  genG10       -0.0429     1.17    125   -0.0367 9.71e- 1
# ℹ 23 more rows

10.2.1.3 Check Model Assumptions

Let’s verify the assumption of linear mixed models including normal distribution and constant variance of residuals.

lme4

check_model(model_icbd, check = c('qq', 'linearity', 'reqq'), detrend=FALSE, alpha =0)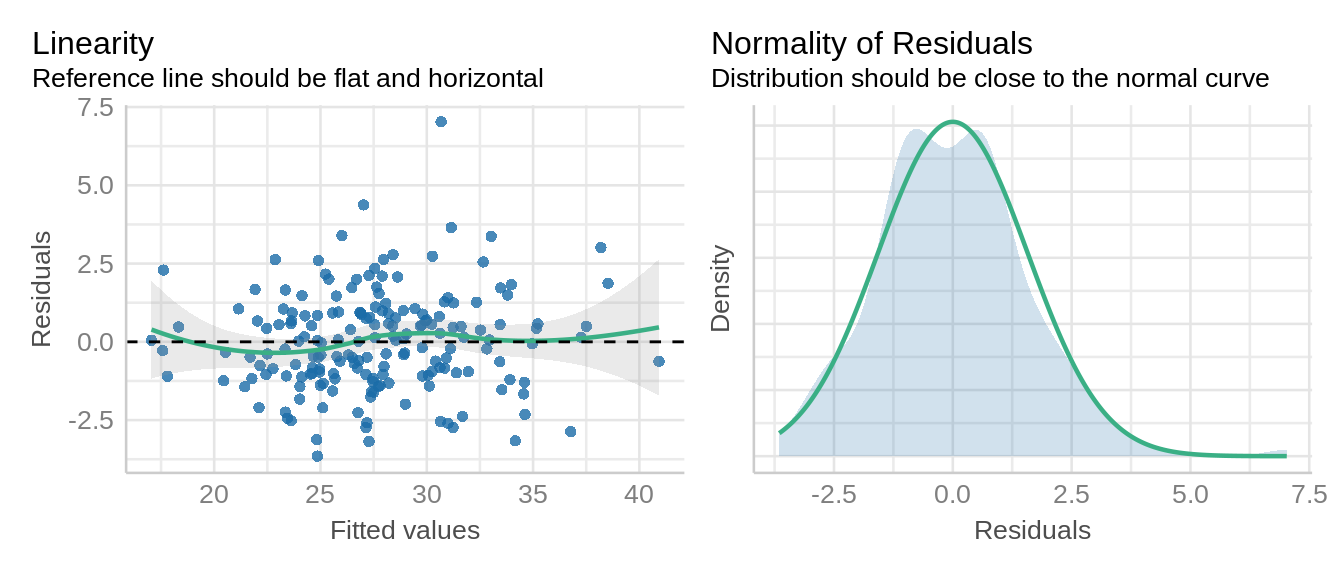

nlme

check_model(model_icbd1, check = c('qq', 'linearity'), detrend=FALSE, alpha = 0)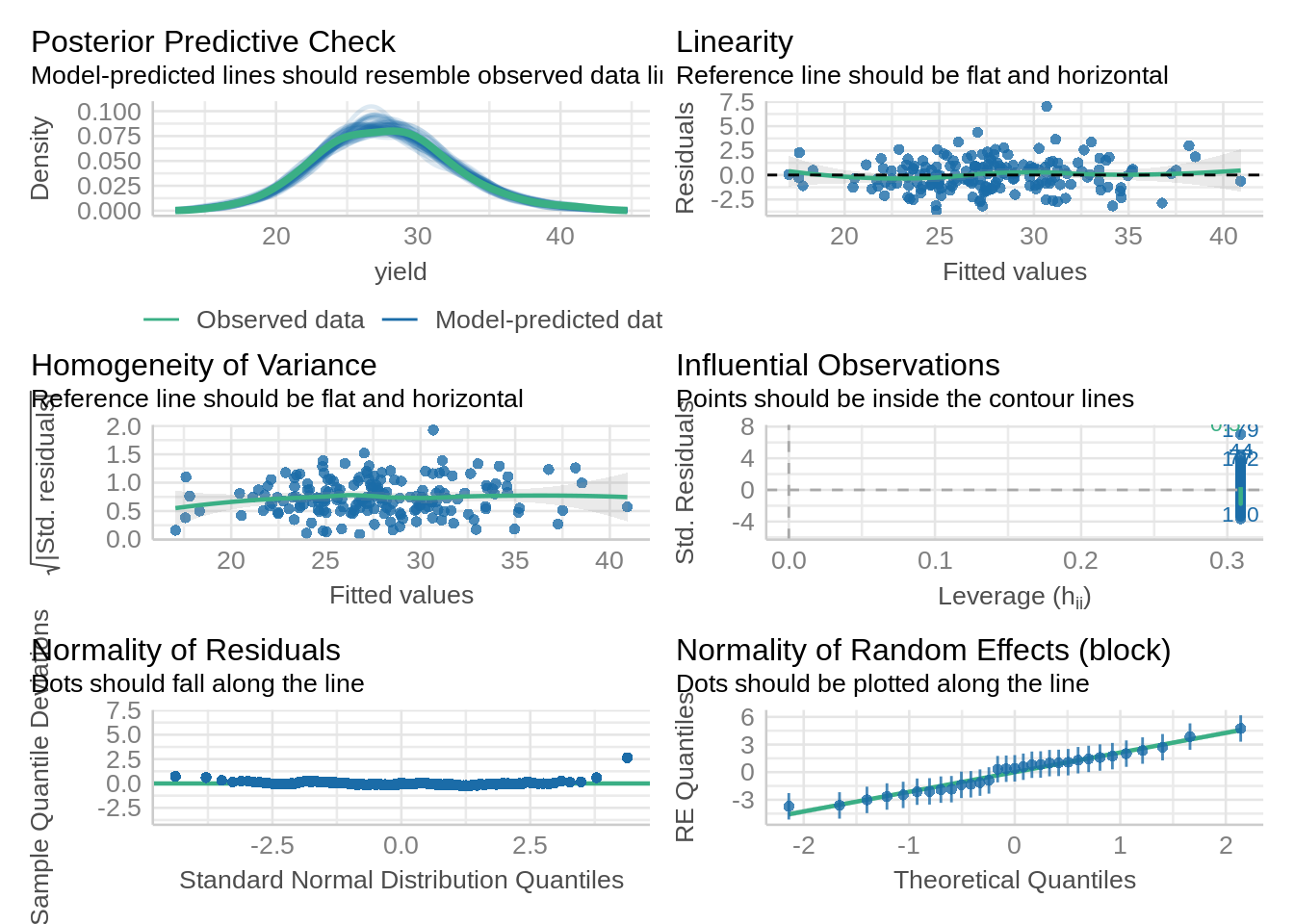

10.2.1.4 Inference

We can extract information about ANOVA using anova().

lme4

anova(model_icbd, type = "1")

Type I Analysis of Variance Table with Satterthwaite's method
    Sum Sq Mean Sq NumDF  DenDF F value    Pr(>F)    
gen 1901.1  63.369    30 129.06  17.675 < 2.2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

nlme

anova(model_icbd1, type = "sequential")

            numDF denDF  F-value p-value
(Intercept)     1   125 4042.016  <.0001
gen            30   125   17.675  <.0001

Let’s look at the estimated marginal means of yield for each variety (gen).

lme4

emmeans(model_icbd, ~ gen)

 gen emmean    SE  df lower.CL upper.CL
 G01   24.6 0.923 153     22.7     26.4
 G02   27.0 0.923 153     25.2     28.8
 G03   32.6 0.923 153     30.8     34.4
 G04   26.9 0.923 153     25.1     28.8
 G05   26.2 0.923 153     24.4     28.0
 G06   32.0 0.923 153     30.1     33.8
 G07   24.2 0.923 153     22.3     26.0
 G08   27.6 0.923 153     25.8     29.4
 G09   29.4 0.923 153     27.6     31.2
 G10   24.5 0.923 153     22.7     26.4
 G11   27.1 0.923 153     25.2     28.9
 G12   29.3 0.923 153     27.4     31.1
 G13   29.9 0.923 153     28.1     31.8
 G14   24.2 0.923 153     22.4     26.1
 G15   26.1 0.923 153     24.3     27.9
 G16   25.9 0.923 153     24.1     27.8
 G17   19.7 0.923 153     17.9     21.5
 G18   25.7 0.923 153     23.9     27.5
 G19   29.0 0.923 153     27.2     30.9
 G20   33.2 0.923 153     31.3     35.0
 G21   31.1 0.923 153     29.3     32.9
 G22   25.2 0.923 153     23.3     27.0
 G23   29.8 0.923 153     28.0     31.6
 G24   33.6 0.923 153     31.8     35.5
 G25   27.0 0.923 153     25.2     28.8
 G26   27.1 0.923 153     25.3     29.0
 G27   23.8 0.923 153     22.0     25.6
 G28   26.5 0.923 153     24.6     28.3
 G29   24.8 0.923 153     22.9     26.6
 G30   36.2 0.923 153     34.4     38.0
 G31   27.1 0.923 153     25.3     28.9

Degrees-of-freedom method: kenward-roger 
Confidence level used: 0.95 

nlme

emmeans(model_icbd1, ~ gen)

 gen emmean    SE df lower.CL upper.CL
 G01   24.6 0.922 30     22.7     26.5
 G02   27.0 0.922 30     25.1     28.9
 G03   32.6 0.922 30     30.7     34.5
 G04   26.9 0.922 30     25.1     28.8
 G05   26.2 0.922 30     24.3     28.1
 G06   32.0 0.922 30     30.1     33.8
 G07   24.2 0.922 30     22.3     26.0
 G08   27.6 0.922 30     25.7     29.5
 G09   29.4 0.922 30     27.5     31.3
 G10   24.5 0.922 30     22.6     26.4
 G11   27.1 0.922 30     25.2     28.9
 G12   29.3 0.922 30     27.4     31.1
 G13   29.9 0.922 30     28.1     31.8
 G14   24.2 0.922 30     22.4     26.1
 G15   26.1 0.922 30     24.2     28.0
 G16   25.9 0.922 30     24.0     27.8
 G17   19.7 0.922 30     17.8     21.6
 G18   25.7 0.922 30     23.8     27.6
 G19   29.0 0.922 30     27.2     30.9
 G20   33.2 0.922 30     31.3     35.0
 G21   31.1 0.922 30     29.2     33.0
 G22   25.2 0.922 30     23.3     27.1
 G23   29.8 0.922 30     27.9     31.7
 G24   33.6 0.922 30     31.8     35.5
 G25   27.0 0.922 30     25.1     28.9
 G26   27.1 0.922 30     25.3     29.0
 G27   23.8 0.922 30     21.9     25.7
 G28   26.5 0.922 30     24.6     28.4
 G29   24.8 0.922 30     22.9     26.6
 G30   36.2 0.922 30     34.3     38.1
 G31   27.1 0.922 30     25.2     29.0

Degrees-of-freedom method: containment 
Confidence level used: 0.95 

10.2.2 Partially Balanced IBD (Alpha Lattice Design)

The statistical model for partially balanced design includes:

\[y_{ij(l)} = \mu + \alpha_i + \beta_{i(l)} + \tau_j + \epsilon_{ij(l)}\]

Where:

\(\mu\) = overall experimental mean
\(\alpha\) = replicate effect (random)
\(\beta\) = incomplete block effect (random)
\(\tau\) = treatment effect (fixed)
\(\epsilon_{ij(l)}\) = intra-block residual

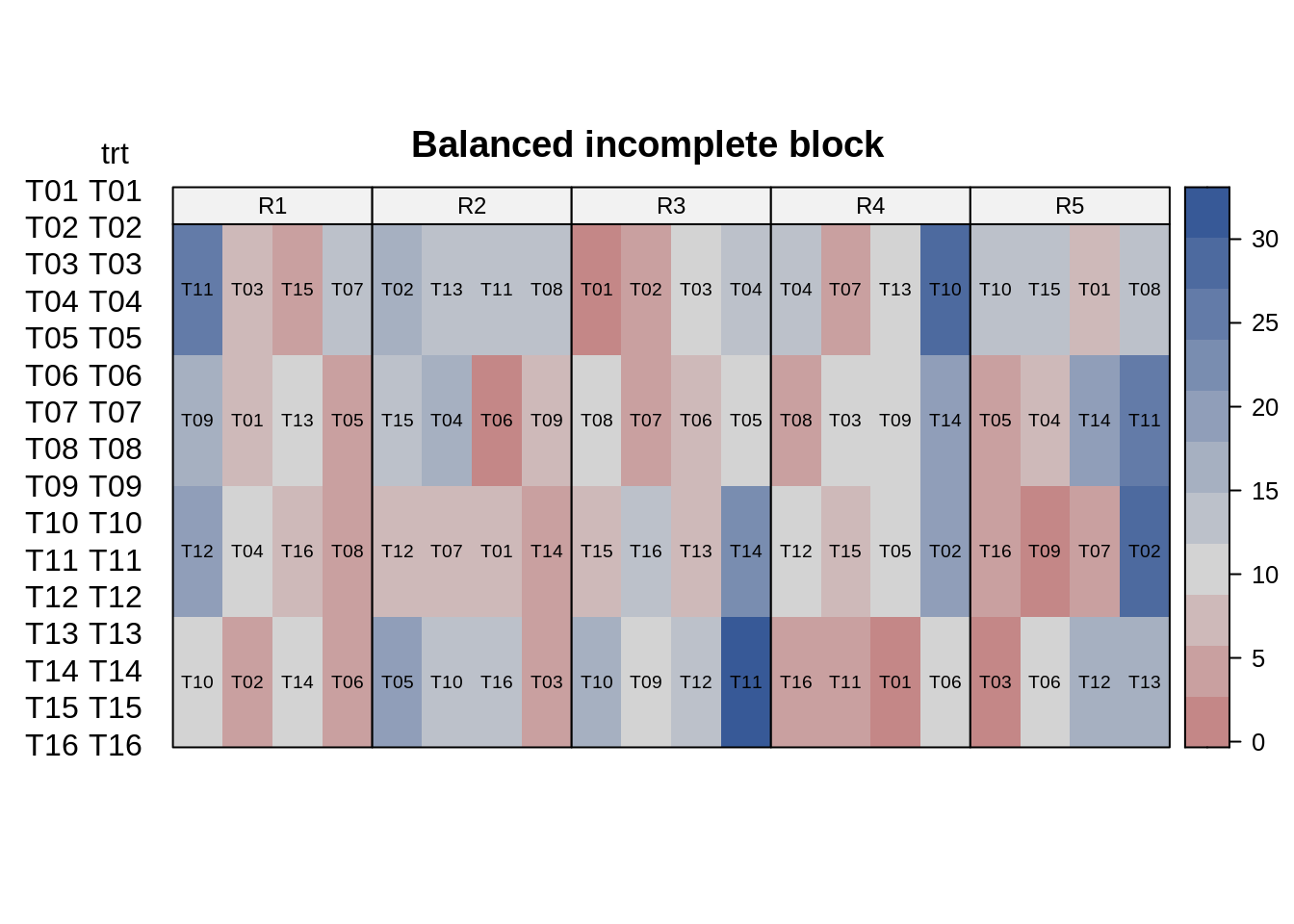
The data used in this example is published in Cyclic and Computer Generated Designs (John and Williams 1995). The trial was laid out in an alpha lattice design. This trial data had 24 genotypes (“gen”), 6 incomplete blocks, each replicated 3 times.

Let’s start analyzing this example first by loading the required libraries for linear mixed models:

lme4

library(lme4); library(lmerTest); library(emmeans)
library(dplyr); library(broom.mixed); library(performance)

nlme

library(nlme); library(broom.mixed); library(emmeans)
library(dplyr); library(performance)

Let’s import a data with partial balanced icomplete design. This data was obtained from the agridat package.

p_icb <- read.csv(here::here("data", "partial_incblock.csv"))

Table of variables in the data set

block	incomplete blocking unit
gen	genotype (variety) factor
row	row position for each plot
col	column position for each plot
yield	grain yield in tonnes/ha

10.2.2.1 Data integrity checks

• Check structure of the data

Let’s look into the structure of the data first to verify the class of the variables.

str(p_icb)

'data.frame':   72 obs. of  7 variables:
 $ plot : int  1 2 3 4 5 6 7 8 9 10 ...
 $ rep  : chr  "R1" "R1" "R1" "R1" ...
 $ block: chr  "B1" "B1" "B1" "B1" ...
 $ gen  : chr  "G11" "G04" "G05" "G22" ...
 $ yield: num  4.12 4.45 5.88 4.58 4.65 ...
 $ row  : int  1 2 3 4 5 6 7 8 9 10 ...
 $ col  : int  1 1 1 1 1 1 1 1 1 1 ...

Here, rep, block and gen are character and yield as a integer. We can continue with this.

• Inspect the independent variables

Next step is to evaluate the independent variables. First, check the number of treatments per replication (each treatment should be replicated 3 times).

agg_tbl <- p_icb %>% group_by(gen) %>% 
  summarise(total_count=n(),
            .groups = 'drop')
agg_tbl

# A tibble: 24 × 2
   gen   total_count
   <chr>       <int>
 1 G01             3
 2 G02             3
 3 G03             3
 4 G04             3
 5 G05             3
 6 G06             3
 7 G07             3
 8 G08             3
 9 G09             3
10 G10             3
# ℹ 14 more rows

This looks balanced, as expected. Also, let’s have a look at the number of times each treatment appear per block.

(agg_blk <- aggregate(p_icb$gen, by=list(p_icb$block), FUN=length))

  Group.1  x
1      B1 12
2      B2 12
3      B3 12
4      B4 12
5      B5 12
6      B6 12

12 treatments randomly appear in incomplete block. Each incomplete block has same number of treatments.

• Check the extent of missing data

colSums(is.na(p_icb))

 plot   rep block   gen yield   row   col 
    0     0     0     0     0     0     0 

No missing values in data!

• Inspect the dependent variable

Before fitting the model, it’s a good idea to look at the distribution of dependent variable, yield.

Figure 10.2: Histogram of the dependent variable.

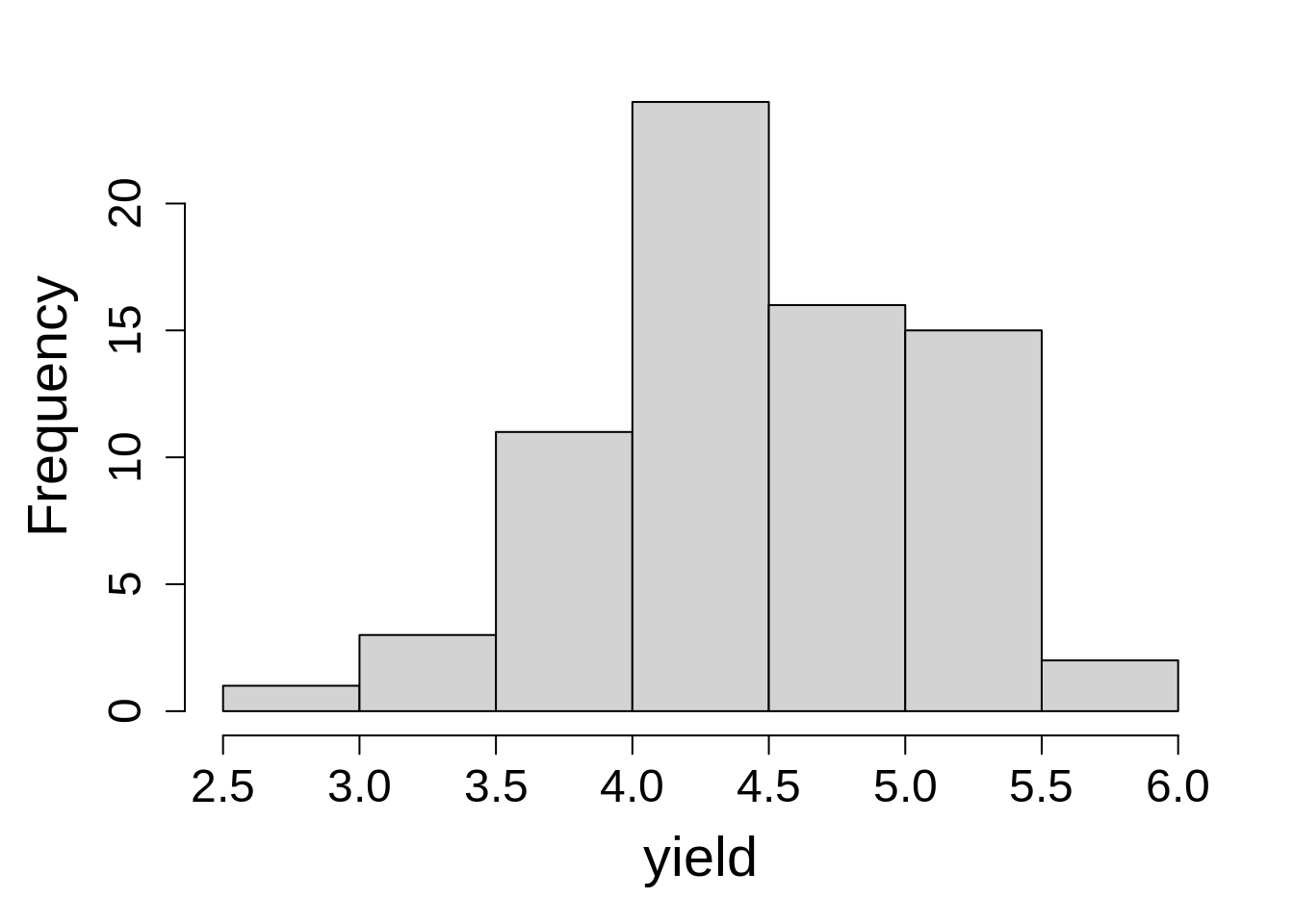
hist(p_icb$yield, main = NA, xlab = "yield")

The response variables seems to follow a normal distribution curve, with few values on extreme lower and higher ends.

10.2.2.2 Model Building

We are evaluating the response of yield to Gen (fixed effect) and rep and block as a random effect.

lme4

mod_alpha <- lmer(yield ~ gen + (1|rep/block),
                   data = p_icb, 
                   na.action = na.exclude)
tidy(mod_alpha)

# A tibble: 27 × 8
   effect group term        estimate std.error statistic    df     p.value
   <chr>  <chr> <chr>          <dbl>     <dbl>     <dbl> <dbl>       <dbl>
 1 fixed  <NA>  (Intercept)   5.11       0.276    18.5    6.19 0.00000118 
 2 fixed  <NA>  genG02       -0.629      0.269    -2.34  38.2  0.0248     
 3 fixed  <NA>  genG03       -1.61       0.268    -6.00  37.7  0.000000590
 4 fixed  <NA>  genG04       -0.618      0.268    -2.30  37.7  0.0269     
 5 fixed  <NA>  genG05       -0.0705     0.258    -0.274 34.8  0.786      
 6 fixed  <NA>  genG06       -0.571      0.268    -2.13  37.7  0.0398     
 7 fixed  <NA>  genG07       -0.997      0.258    -3.87  34.8  0.000457   
 8 fixed  <NA>  genG08       -0.580      0.268    -2.16  37.7  0.0370     
 9 fixed  <NA>  genG09       -1.61       0.258    -6.21  35.3  0.000000390
10 fixed  <NA>  genG10       -0.735      0.259    -2.83  35.9  0.00754    
# ℹ 17 more rows

nlme

mod_alpha1 <- lme(yield ~ gen,
                  random = ~ 1|rep/block,
                  data = p_icb, 
                  na.action = na.exclude)
tidy(mod_alpha1)

Warning in tidy.lme(mod_alpha1): ran_pars not yet implemented for multiple
levels of nesting

# A tibble: 24 × 7
   effect term        estimate std.error    df statistic  p.value
   <chr>  <chr>          <dbl>     <dbl> <dbl>     <dbl>    <dbl>
 1 fixed  (Intercept)   5.11       0.276    31    18.5   2.63e-18
 2 fixed  genG02       -0.629      0.269    31    -2.34  2.61e- 2
 3 fixed  genG03       -1.61       0.268    31    -6.00  1.23e- 6
 4 fixed  genG04       -0.618      0.268    31    -2.30  2.81e- 2
 5 fixed  genG05       -0.0705     0.258    31    -0.274 7.86e- 1
 6 fixed  genG06       -0.571      0.268    31    -2.13  4.12e- 2
 7 fixed  genG07       -0.997      0.258    31    -3.87  5.23e- 4
 8 fixed  genG08       -0.580      0.268    31    -2.16  3.84e- 2
 9 fixed  genG09       -1.61       0.258    31    -6.21  6.71e- 7
10 fixed  genG10       -0.735      0.259    31    -2.83  8.05e- 3
# ℹ 14 more rows

10.2.2.3 Check Model Assumptions

Let’s verify the assumption of linear mixed models including normal distribution and constant variance of residuals.

lme4

check_model(mod_alpha, check = c('qq', 'linearity', 'reqq'), detrend=FALSE, alpha = 0)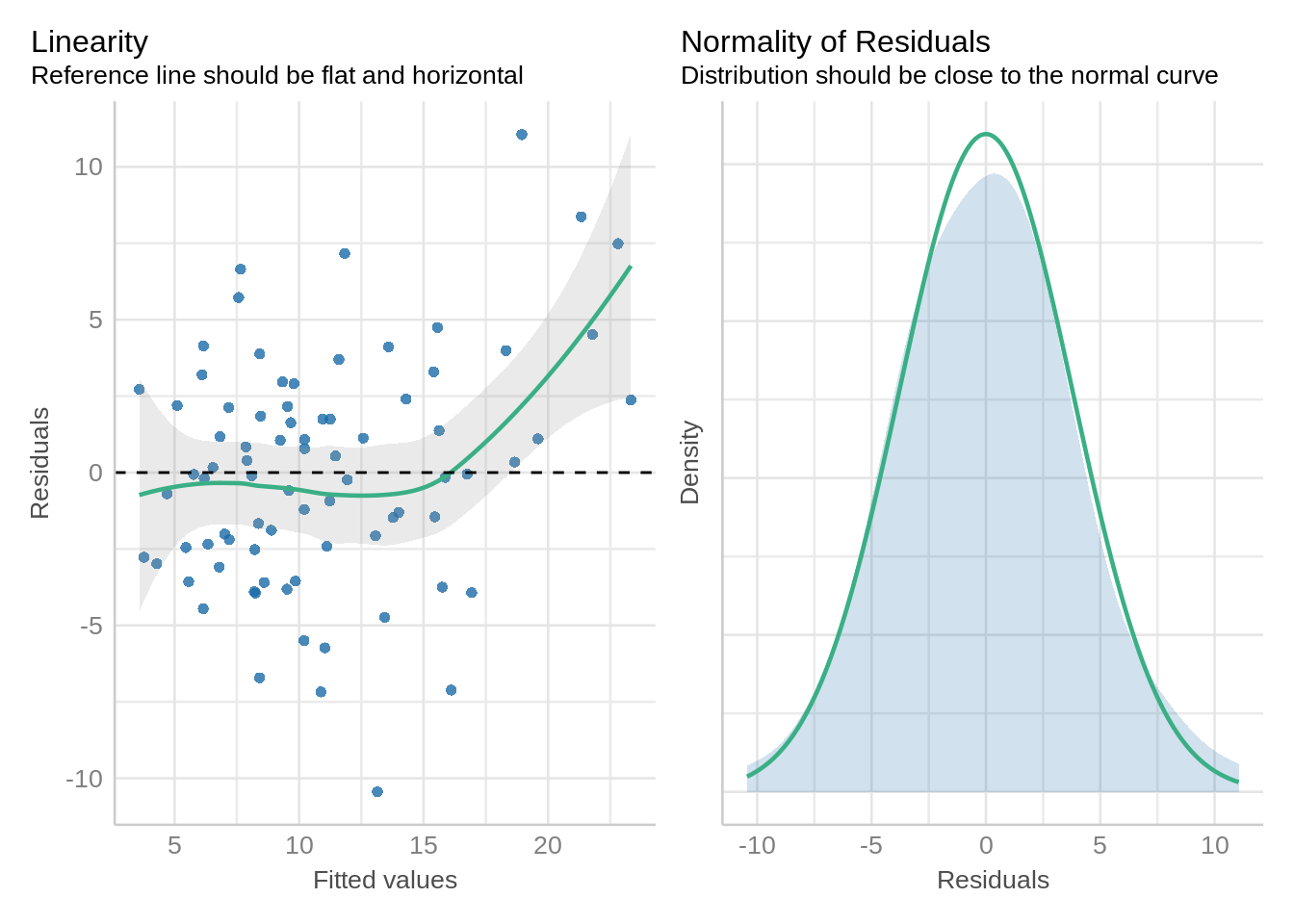

nlme

check_model(mod_alpha1, check = c('qq', 'linearity'), detrend=FALSE, alpha = 0)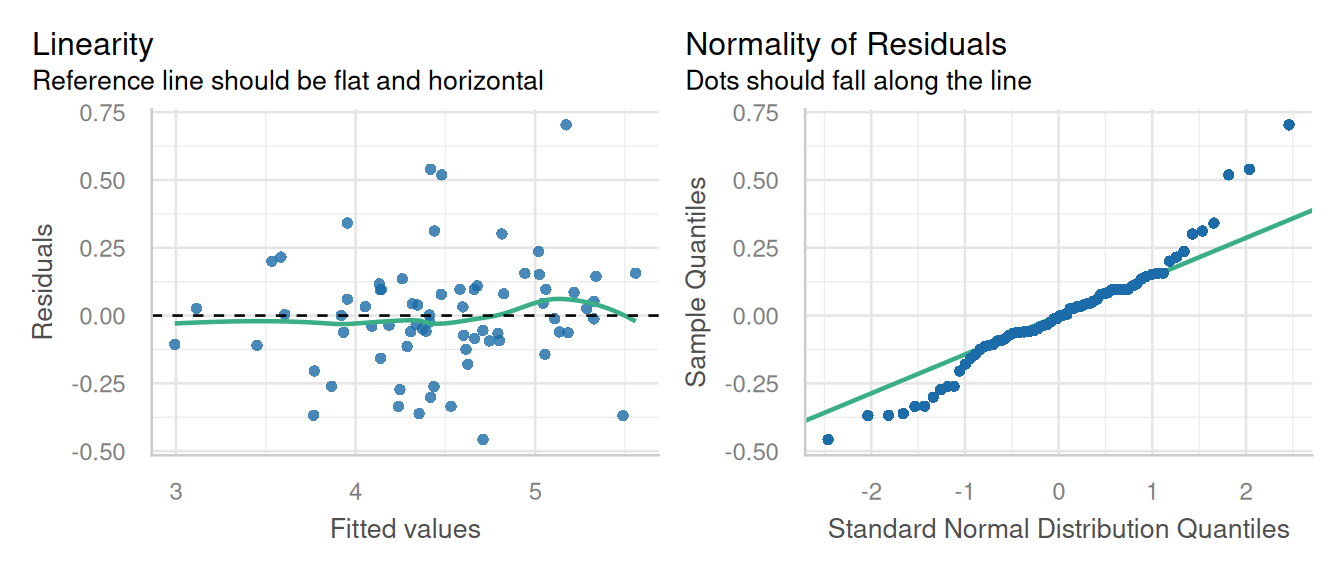

Here a little skewness is present normality of residuals, but that’s not a major deviation in the model assumptions.

10.2.2.4 Inference

Let’s look at the ANOVA table using anova() from lmer and lme models, respectively.

lme4

anova(mod_alpha, type = "1")

Type I Analysis of Variance Table with Satterthwaite's method
    Sum Sq Mean Sq NumDF  DenDF F value    Pr(>F)    
gen 10.679 0.46429    23 34.902  5.4478 4.229e-06 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

nlme

anova(mod_alpha1, type = "sequential")

            numDF denDF  F-value p-value
(Intercept)     1    31 470.9507  <.0001
gen            23    31   5.4478  <.0001

Let’s look at the estimated marginal means of yield for each variety (gen).

lme4

emmeans(mod_alpha, ~ gen)

 gen emmean    SE   df lower.CL upper.CL
 G01   5.11 0.279 6.20     4.43     5.78
 G02   4.48 0.279 6.20     3.80     5.15
 G03   3.50 0.279 6.20     2.82     4.18
 G04   4.49 0.279 6.20     3.81     5.17
 G05   5.04 0.278 6.19     4.36     5.71
 G06   4.54 0.278 6.19     3.86     5.21
 G07   4.11 0.279 6.20     3.43     4.79
 G08   4.53 0.279 6.20     3.85     5.20
 G09   3.50 0.278 6.19     2.83     4.18
 G10   4.37 0.279 6.20     3.70     5.05
 G11   4.28 0.279 6.20     3.61     4.96
 G12   4.76 0.279 6.20     4.08     5.43
 G13   4.76 0.278 6.19     4.08     5.43
 G14   4.78 0.278 6.19     4.10     5.45
 G15   4.97 0.278 6.19     4.29     5.65
 G16   4.73 0.279 6.20     4.05     5.41
 G17   4.60 0.278 6.19     3.93     5.28
 G18   4.36 0.279 6.20     3.69     5.04
 G19   4.84 0.278 6.19     4.16     5.52
 G20   4.04 0.278 6.19     3.36     4.72
 G21   4.80 0.278 6.19     4.12     5.47
 G22   4.53 0.278 6.19     3.85     5.20
 G23   4.25 0.278 6.19     3.58     4.93
 G24   4.15 0.279 6.20     3.48     4.83

Degrees-of-freedom method: kenward-roger 
Confidence level used: 0.95 

nlme

emmeans(mod_alpha1, ~ gen)

 gen emmean    SE df lower.CL upper.CL
 G01   5.11 0.276  2     3.92     6.30
 G02   4.48 0.276  2     3.29     5.67
 G03   3.50 0.276  2     2.31     4.69
 G04   4.49 0.276  2     3.30     5.68
 G05   5.04 0.276  2     3.85     6.22
 G06   4.54 0.276  2     3.35     5.72
 G07   4.11 0.276  2     2.92     5.30
 G08   4.53 0.276  2     3.34     5.72
 G09   3.50 0.276  2     2.31     4.69
 G10   4.37 0.276  2     3.19     5.56
 G11   4.28 0.276  2     3.10     5.47
 G12   4.76 0.276  2     3.57     5.94
 G13   4.76 0.276  2     3.57     5.95
 G14   4.78 0.276  2     3.59     5.96
 G15   4.97 0.276  2     3.78     6.16
 G16   4.73 0.276  2     3.54     5.92
 G17   4.60 0.276  2     3.42     5.79
 G18   4.36 0.276  2     3.17     5.55
 G19   4.84 0.276  2     3.65     6.03
 G20   4.04 0.276  2     2.85     5.23
 G21   4.80 0.276  2     3.61     5.98
 G22   4.53 0.276  2     3.34     5.72
 G23   4.25 0.276  2     3.06     5.44
 G24   4.15 0.276  2     2.97     5.34

Degrees-of-freedom method: containment 
Confidence level used: 0.95 

John, JA, and ER Williams. 1995. Cyclic and Computer Generated Designs. 2nd ed. New York: Chapman; Hall/CRC Press. https://doi.org/10.1201/b15075.

Meier, Lukas. 2022. ANOVA and Mixed Models. New York: Chapman; Hall/CRC. https://doi.org/https://doi.org/10.1201/9781003146216 .

Nair, K. R. 1952. “Analysis of Partially Balanced Incomplete Block Designs Illustrated on the Simple Square and Rectangular Lattices.” Biometrics 8 (2): 122–55. https://doi.org/10.2307/3001929.

Oehlert, Gary W. 2000. Mixed-Effects Models in s and s-PLUS. New York: W.H. Freeman. http://users.stat.umn.edu/~gary/book/fcdae.pdf.

Patterson, H. D., and E. R. Williams. 1976. “A New Class of Resolvable Incomplete Block Designs.” Biometrika 63 (1): 83–92. https://doi.org/10.2307/2335087.

Yates, F. 1936. “A New Method of Arranging Variety Trials Involving a Large Number of Varieties.” J Agric Sci 26: 424–55.