library(nlme); library(performance); library(emmeans)
library(dplyr); library(broom.mixed); library(multcompView)
library(multcomp); library(ggplot2)13 Marginal Means & Contrasts
13.1 Background
Estimated marginal means are the means of a response variable averaged across all levels of other variables in a model, conditioned on the variance-covariance matrix. That is to say, these are much more than plain averages. The emmeans package is one of the most commonly used package in R for determining marginal means (also known as least-squares means). In this chapter, we will demonstrate the use of the emmeans package to calculate estimated marginal means and confidence intervals and conduct post-hoc comparisons.
To demonstrate the use of the emmeans package. We will use the model from split plot lesson (Chapter 7), where we evaluated the effect of nitrogen and variety on oat yield. This data contains six blocks, three main plots (Variety) and four subplots (Nitrogen). The dependent variable was oat yield. To read more about the experiment layout details please read RCBD split-plot section in Chapter 7.
For demonstration of the emmeans package, we are fitting model with nlme package. Please note that code below calculating marginal means works for both lmer() and nlme() models.
13.2 Analysis Examples
Let’s start this example by loading the required libraries for fitting linear mixed models using nlme package.
13.2.1 Import data
Next step is to import the oats data from the MASS package.
data1 <- MASS::oatsTo read more about data and model explanation please refer to Chapter 7.
13.2.2 Model fitting
model1 <- lme(Y ~ V + N + V:N ,
random = ~1|B/V,
data = data1,
na.action = na.exclude)
tidy(model1)Warning in tidy.lme(model1): ran_pars not yet implemented for multiple levels
of nesting# A tibble: 12 × 7
effect term estimate std.error df statistic p.value
<chr> <chr> <dbl> <dbl> <dbl> <dbl> <dbl>
1 fixed (Intercept) 80 9.11 45 8.78 2.56e-11
2 fixed VMarvellous 6.67 9.72 10 0.686 5.08e- 1
3 fixed VVictory -8.5 9.72 10 -0.875 4.02e- 1
4 fixed N0.2cwt 18.5 7.68 45 2.41 2.02e- 2
5 fixed N0.4cwt 34.7 7.68 45 4.51 4.58e- 5
6 fixed N0.6cwt 44.8 7.68 45 5.84 5.48e- 7
7 fixed VMarvellous:N0.2cwt 3.33 10.9 45 0.307 7.60e- 1
8 fixed VVictory:N0.2cwt -0.333 10.9 45 -0.0307 9.76e- 1
9 fixed VMarvellous:N0.4cwt -4.17 10.9 45 -0.383 7.03e- 1
10 fixed VVictory:N0.4cwt 4.67 10.9 45 0.430 6.70e- 1
11 fixed VMarvellous:N0.6cwt -4.67 10.9 45 -0.430 6.70e- 1
12 fixed VVictory:N0.6cwt 2.17 10.9 45 0.199 8.43e- 113.2.3 Check Model Assumptions
check_model(model1, check = c('qq', 'linearity'), detrend=FALSE, alpha = 0)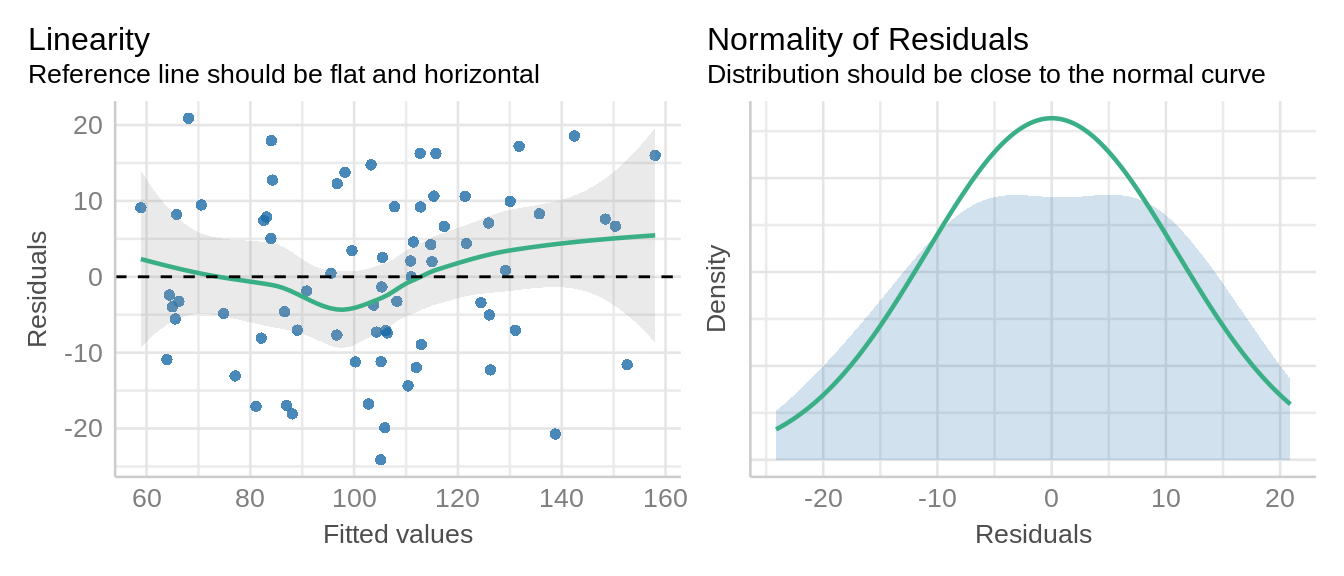
Residuals look good with a small hump in middle and normality curve looks reasonable.
13.2.4 Model Inference
anova(model1, type = "marginal") numDF denDF F-value p-value
(Intercept) 1 45 77.16732 <.0001
V 2 10 1.22454 0.3344
N 3 45 13.02273 <.0001
V:N 6 45 0.30282 0.9322The analysis of variance showed a significant N effect and no effect of V and V x N interaction effect on oat yield.
13.2.5 Estimated Marginal Means
Now that we have fitted a linear mixed model (model1) and it meets the model assumptions, we can use the emmeans() function to obtain estimated marginal means for main effects (variety and nitrogen) and interaction (variety x nitrogen).
13.2.5.1 Main effects
The main effects in model1 were V and N.
m1 <- emmeans(model1, ~V, level = 0.95)NOTE: Results may be misleading due to involvement in interactionsm1 V emmean SE df lower.CL upper.CL
Golden.rain 104.5 7.8 5 84.5 125
Marvellous 109.8 7.8 5 89.7 130
Victory 97.6 7.8 5 77.6 118
Results are averaged over the levels of: N
Degrees-of-freedom method: containment
Confidence level used: 0.95 m2 <- emmeans(model1, ~N)NOTE: Results may be misleading due to involvement in interactionsm2 N emmean SE df lower.CL upper.CL
0.0cwt 79.4 7.17 5 60.9 97.8
0.2cwt 98.9 7.17 5 80.4 117.3
0.4cwt 114.2 7.17 5 95.8 132.7
0.6cwt 123.4 7.17 5 104.9 141.8
Results are averaged over the levels of: V
Degrees-of-freedom method: containment
Confidence level used: 0.95 Make sure to read and interpret marginal means carefully. Here, when we calculated marginal means for main effects of V and N, these were averaged over the levels of other factor in experiment. For example, estimated means for each variety were averaged over the N treatments.
13.2.5.2 Interaction effects
Now let’s evaluate the marginal means for the interaction effect of V and N. These can be calculated either using V*N or V|N format.
m3 <- emmeans(model1, ~V|N)
m3N = 0.0cwt:
V emmean SE df lower.CL upper.CL
Golden.rain 80.0 9.11 5 56.6 103.4
Marvellous 86.7 9.11 5 63.3 110.1
Victory 71.5 9.11 5 48.1 94.9
N = 0.2cwt:
V emmean SE df lower.CL upper.CL
Golden.rain 98.5 9.11 5 75.1 121.9
Marvellous 108.5 9.11 5 85.1 131.9
Victory 89.7 9.11 5 66.3 113.1
N = 0.4cwt:
V emmean SE df lower.CL upper.CL
Golden.rain 114.7 9.11 5 91.3 138.1
Marvellous 117.2 9.11 5 93.8 140.6
Victory 110.8 9.11 5 87.4 134.2
N = 0.6cwt:
V emmean SE df lower.CL upper.CL
Golden.rain 124.8 9.11 5 101.4 148.2
Marvellous 126.8 9.11 5 103.4 150.2
Victory 118.5 9.11 5 95.1 141.9
Degrees-of-freedom method: containment
Confidence level used: 0.95 m4 <- emmeans(model1, ~V*N)
m4 V N emmean SE df lower.CL upper.CL
Golden.rain 0.0cwt 80.0 9.11 5 56.6 103.4
Marvellous 0.0cwt 86.7 9.11 5 63.3 110.1
Victory 0.0cwt 71.5 9.11 5 48.1 94.9
Golden.rain 0.2cwt 98.5 9.11 5 75.1 121.9
Marvellous 0.2cwt 108.5 9.11 5 85.1 131.9
Victory 0.2cwt 89.7 9.11 5 66.3 113.1
Golden.rain 0.4cwt 114.7 9.11 5 91.3 138.1
Marvellous 0.4cwt 117.2 9.11 5 93.8 140.6
Victory 0.4cwt 110.8 9.11 5 87.4 134.2
Golden.rain 0.6cwt 124.8 9.11 5 101.4 148.2
Marvellous 0.6cwt 126.8 9.11 5 103.4 150.2
Victory 0.6cwt 118.5 9.11 5 95.1 141.9
Degrees-of-freedom method: containment
Confidence level used: 0.95 Here, note that we estimated marginal means in two ways:
V*N estimates the marginal means for each combination of levels across these variables, and when conducting pairwise comparisons on these, all combinations are compared to one another simultaneously (not recommended).
V|N estimates the marginal means for each V at a given level of N. When conducting pairwise comparisons on these, all levels of the variable V are compared with each other within each level of N, not across all levels of N (a sensible approach).
13.3 Contrasts using emmeans
The pairs() function from the emmeans package can be used to evaluate pairwise comparisons among treatment factors. The emmean object (m1, m2) will be passed through the pairs() function, which will provide a p-value adjustment equivalent to the Tukey test.
pairs(m1, adjust = "tukey") contrast estimate SE df t.ratio p.value
Golden.rain - Marvellous -5.29 7.08 10 -0.748 0.7419
Golden.rain - Victory 6.88 7.08 10 0.971 0.6104
Marvellous - Victory 12.17 7.08 10 1.719 0.2458
Results are averaged over the levels of: N
Degrees-of-freedom method: containment
P value adjustment: tukey method for comparing a family of 3 estimates pairs(m2) contrast estimate SE df t.ratio p.value
0.0cwt - 0.2cwt -19.50 4.44 45 -4.396 0.0004
0.0cwt - 0.4cwt -34.83 4.44 45 -7.853 <.0001
0.0cwt - 0.6cwt -44.00 4.44 45 -9.919 <.0001
0.2cwt - 0.4cwt -15.33 4.44 45 -3.457 0.0064
0.2cwt - 0.6cwt -24.50 4.44 45 -5.523 <.0001
0.4cwt - 0.6cwt -9.17 4.44 45 -2.067 0.1797
Results are averaged over the levels of: V
Degrees-of-freedom method: containment
P value adjustment: tukey method for comparing a family of 4 estimates The more levels in a variable, the more comparisons that are conducted, reducing statistical power due to the p-value adjustment used to limit type I error.
pairs()
This function conducts all pairwise tests for the specified variable specified. The default p-value adjustment in the pairs() function is “tukey”; other options include “holm”, “hochberg”, “BH”, “BY”, and “none”. If you are conducting this on a variable with many levels (e.g. more than five), this adjustment can be severe, resulting in very few statistically significant results. To avoid this, consider other tests such as ‘compare to a control’ or more tailored custom contrasts.
13.3.1 Custom contrasts
Custom contrast in statistics refer to specific comparisons between groups as defined by researcher before analyzing the data. This allows us to test the particular research hypothesis, for example to compare treatment A vs B or treatment A vs C. These are linear combination of treatment means where we assign specific weights to each grouping depending on our hypothesis. The condition for custom contrasts is that the weights must sum to zero.
Here, we will demonstrate the steps to build custom contrasts for comparing nitrogen treatment A1 to A2, A3, and A4, separately.
First, run emmeans object ‘m2’ for nitrogen treatments.
m2 N emmean SE df lower.CL upper.CL
0.0cwt 79.4 7.17 5 60.9 97.8
0.2cwt 98.9 7.17 5 80.4 117.3
0.4cwt 114.2 7.17 5 95.8 132.7
0.6cwt 123.4 7.17 5 104.9 141.8
Results are averaged over the levels of: V
Degrees-of-freedom method: containment
Confidence level used: 0.95 Now, let’s create a vector for each nitrogen treatment in the same order as presented in output from m2.
A1 = c(1, 0, 0, 0)
A2 = c(0, 1, 0, 0)
A3 = c(0, 0, 1, 0)
A4 = c(0, 0, 0, 1)These vectors (A1, A2, A3, A4) represent each nitrogen treatment in the order as presented in the m2 emmeans object. A1, A2, A3, and A4 vectors represent 0.0 cwt, 0.2 cwt, 0.4 cwt, and 0.6 cwt nitrogen treatments, respectively.
The next step is to create custom contrasts for comparing ‘0.0cwt’ (A1) treatment to ‘0.2cwt’ (A2), ‘0.4cwt’ (A3), and ‘0.6cwt’ (A4) treatments.
contrast(m2, method = list(A1 - A2) ) contrast estimate SE df t.ratio p.value
c(1, -1, 0, 0) -19.5 4.44 45 -4.396 0.0001
Results are averaged over the levels of: V
Degrees-of-freedom method: containment contrast(m2, method = list(A1 - A3) ) contrast estimate SE df t.ratio p.value
c(1, 0, -1, 0) -34.8 4.44 45 -7.853 <.0001
Results are averaged over the levels of: V
Degrees-of-freedom method: containment contrast(m2, method = list(A1 - A4) ) contrast estimate SE df t.ratio p.value
c(1, 0, 0, -1) -44 4.44 45 -9.919 <.0001
Results are averaged over the levels of: V
Degrees-of-freedom method: containment The output shows the difference in mean yield between the control and the three N treatments. The results show that yield increased with nitrogen treatments compared to the control (0.0 cwt) irrespective of the oat variety.
In addition to these custom contrast options, we can also use the built-in functions in the emmeans package to compare treatments as per our analysis objectives. For example, comparing treatments to control or to compare one treatment level to all other groups.
We will start with examining m1, an emmeans object.
m1 V emmean SE df lower.CL upper.CL
Golden.rain 104.5 7.8 5 84.5 125
Marvellous 109.8 7.8 5 89.7 130
Victory 97.6 7.8 5 77.6 118
Results are averaged over the levels of: N
Degrees-of-freedom method: containment
Confidence level used: 0.95 Let’s suppose we want to compare ‘Marvellous’ with the other varieties in the analysis. We can conduct “treatment v control” contrasts, setting the variety ‘Marvellous’ as the control with the ref argument.
contrast(m1, "trt.vs.ctrl", ref = "Marvellous") contrast estimate SE df t.ratio p.value
Golden.rain - Marvellous -5.29 7.08 10 -0.748 0.6833
Victory - Marvellous -12.17 7.08 10 -1.719 0.2045
Results are averaged over the levels of: N
Degrees-of-freedom method: containment
P value adjustment: dunnettx method for 2 tests Alternatively, we can reference the control group by its appearance in the variety order. In m1, ‘Golden rain’, ‘Marvellous’, and ‘Victory’ are ordered as 1, 2, and 3 respectively.1
1 This follow an alphabetic ordering that can be altered with the factor() function.
If we want to contrast ‘Golden rain’ with other varieties, we can do this by either using trt.vs.ctrl1 code, or trt.vs.ctrlk and referring to group 1. Both code options will generate the same results.
contrast(m1, "trt.vs.ctrl1") contrast estimate SE df t.ratio p.value
Marvellous - Golden.rain 5.29 7.08 10 0.748 0.6833
Victory - Golden.rain -6.88 7.08 10 -0.971 0.5476
Results are averaged over the levels of: N
Degrees-of-freedom method: containment
P value adjustment: dunnettx method for 2 tests contrast(m1, "trt.vs.ctrlk", ref = 1) contrast estimate SE df t.ratio p.value
Marvellous - Golden.rain 5.29 7.08 10 0.748 0.6833
Victory - Golden.rain -6.88 7.08 10 -0.971 0.5476
Results are averaged over the levels of: N
Degrees-of-freedom method: containment
P value adjustment: dunnettx method for 2 tests We can further customize the contrasts by excluding specific treatment groups from the comparison.
we can demonstrate this by printing the m2 object first to check the treatment order:
m2 N emmean SE df lower.CL upper.CL
0.0cwt 79.4 7.17 5 60.9 97.8
0.2cwt 98.9 7.17 5 80.4 117.3
0.4cwt 114.2 7.17 5 95.8 132.7
0.6cwt 123.4 7.17 5 104.9 141.8
Results are averaged over the levels of: V
Degrees-of-freedom method: containment
Confidence level used: 0.95 Next, we can conduct a pairwise comparison by excluding 0.2 cwt.
pairs(m2, exclude = 2) contrast estimate SE df t.ratio p.value
0.0cwt - 0.4cwt -34.83 4.44 45 -7.853 <.0001
0.0cwt - 0.6cwt -44.00 4.44 45 -9.919 <.0001
0.4cwt - 0.6cwt -9.17 4.44 45 -2.067 0.1084
Results are averaged over the levels of: V
Degrees-of-freedom method: containment
P value adjustment: tukey method for comparing a family of 3 estimates Or we can also evaluate consecutive pairwise comparison as follows:
contrast(m2, "consec") contrast estimate SE df t.ratio p.value
0.2cwt - 0.0cwt 19.50 4.44 45 4.396 0.0002
0.4cwt - 0.2cwt 15.33 4.44 45 3.457 0.0036
0.6cwt - 0.4cwt 9.17 4.44 45 2.067 0.1153
Results are averaged over the levels of: V
Degrees-of-freedom method: containment
P value adjustment: mvt method for 3 tests 13.4 Compact letter displays
Compact letter display (CLD) is a widely used tool by researchers to show multiple comparisons among treatment means. However, the implementation of CLDs can be problematic depending on the analysis aim and experiment design. This is discussed in detail in the Analysis Tips Chapter. In particular, using CLD to contrast a large number of levels (e.g. 10 or more) often leads to misinterpretation of the results, where people assume items not significantly different from each other are equivalent. It is a good practice in any statistical analysis to carefully consider the research goals before implementing CLDs.
The R package multcompView (2019) can be used to generate a display where any two means associated with same symbol are not statistically different using the function cld().
Below are examples of CLD for objects m1 (examining variety), m2 (examining nitrogen), and m3 (examining variety within each nitrogen group). In the output below, groups sharing a same letter in the \(.group\) are not statistically different from each other.
cld(m1, alpha = 0.05, Letters = letters) V emmean SE df lower.CL upper.CL .group
Victory 97.6 7.8 5 77.6 118 a
Golden.rain 104.5 7.8 5 84.5 125 a
Marvellous 109.8 7.8 5 89.7 130 a
Results are averaged over the levels of: N
Degrees-of-freedom method: containment
Confidence level used: 0.95
P value adjustment: tukey method for comparing a family of 3 estimates
significance level used: alpha = 0.05
NOTE: If two or more means share the same grouping symbol,
then we cannot show them to be different.
But we also did not show them to be the same. cld(m2, alpha = 0.05, Letters = letters) N emmean SE df lower.CL upper.CL .group
0.0cwt 79.4 7.17 5 60.9 97.8 a
0.2cwt 98.9 7.17 5 80.4 117.3 b
0.4cwt 114.2 7.17 5 95.8 132.7 c
0.6cwt 123.4 7.17 5 104.9 141.8 c
Results are averaged over the levels of: V
Degrees-of-freedom method: containment
Confidence level used: 0.95
P value adjustment: tukey method for comparing a family of 4 estimates
significance level used: alpha = 0.05
NOTE: If two or more means share the same grouping symbol,
then we cannot show them to be different.
But we also did not show them to be the same. Let’s have a look at the CLDs for the interaction effect:
cld3 <- cld(m3, alpha = 0.05, Letters = letters)13.5 Alternative Approaches
- Equivalence testing
If your experimental goals include evaluating if two or more treatments are the same or equivalent, you can use equivalence testing. This requires that we first establish a specific threshold value, which is the maximum difference between groups that is not considered meaningful in the given the data set. That is, what is a numerical difference that is not substantial, and if two groups differed by that amount or less, the researcher would not consider that to be a difference that matters. This is a value of judgement informed by domain expertise.
For the next example, we will assume that if the mean difference of two groups differ by less than 30 (specified in delta argument), they can be considered equivalent. We will conduct an equivalence test for all pairwise comparisons of nitrogen treatment emmeans (object m2).
cld(m2, delta = 30, adjust = "none", Letters = letters) N emmean SE df lower.CL upper.CL .equiv.set
0.0cwt 79.4 7.17 5 60.9 97.8 a
0.2cwt 98.9 7.17 5 80.4 117.3 ab
0.4cwt 114.2 7.17 5 95.8 132.7 bc
0.6cwt 123.4 7.17 5 104.9 141.8 c
Results are averaged over the levels of: V
Degrees-of-freedom method: containment
Confidence level used: 0.95
Statistics are tests of equivalence with a threshold of 30
P values are left-tailed
significance level used: alpha = 0.05
Estimates sharing the same symbol test as equivalent Here, two treatment groups 0.0 cwt and 0.2 cwt, 0.4 cwt and 0.6 cwt can be considered equivalent.
- Significance sets
Another option to CLDs is the significance sets with command signif = TRUE in cld() function. In this, means that have same letters are statistically different. This can be a useful method while working with large number of groups.
cld(m2, signif = TRUE) N emmean SE df lower.CL upper.CL .signif.set
0.0cwt 79.4 7.17 5 60.9 97.8 12
0.2cwt 98.9 7.17 5 80.4 117.3 12
0.4cwt 114.2 7.17 5 95.8 132.7 1
0.6cwt 123.4 7.17 5 104.9 141.8 2
Results are averaged over the levels of: V
Degrees-of-freedom method: containment
Confidence level used: 0.95
P value adjustment: tukey method for comparing a family of 4 estimates
significance level used: alpha = 0.05
Estimates sharing the same symbol are significantly different It’s important to note that we cannot conclude that treatment levels with the same letter are equivalent. We can only conclude that they are not different.
There is a separate branch of statistics, equivalence testing, that is for ascertaining if things are sufficiently similar to conclude they are equivalent.
See Section 2.0.4 for additional warnings about problems with using compact l
13.6 Export emmeans to an external file
The outputs from emmeans() or cld() objects can be exported by first converting them to a data frame and using any of the usual export functions (e.g. write.csv())
result_n <- as.data.frame(m1)
write.csv(result_n, "results.csv", row.names = FALSE)13.7 Graphical display of emmeans
On easy option is to use default plotting functions that accompany the emmeans package.
plot(m1)
plot(m3)
#pwpp(m1)Eventually, you will want to create customized plots of model estimates. To do this, the means will have to be manually extracted and converted to a data frame for usage by plotting libraries. The outputs from the cld3 object (yield of variety within each nitrogen level) can be visualized in ggplot, with variety on the x-axis and estimated means of yield on the y-axis. Different N treatments are presented using different colors.
ggplot(cld3) +
aes(x = V, y = emmean, color = N) +
geom_point(position = position_dodge(width = 0.9)) +
geom_errorbar(mapping = aes(ymin = lower.CL, ymax = upper.CL),
position = position_dodge(width = 1),
width = 0.1) +
geom_text(mapping = aes(label = .group, y = upper.CL * 1.05),
position = position_dodge(width = 0.8),
show.legend = F)+
theme_bw()+
theme(axis.text= element_text(color = "black",
size =12))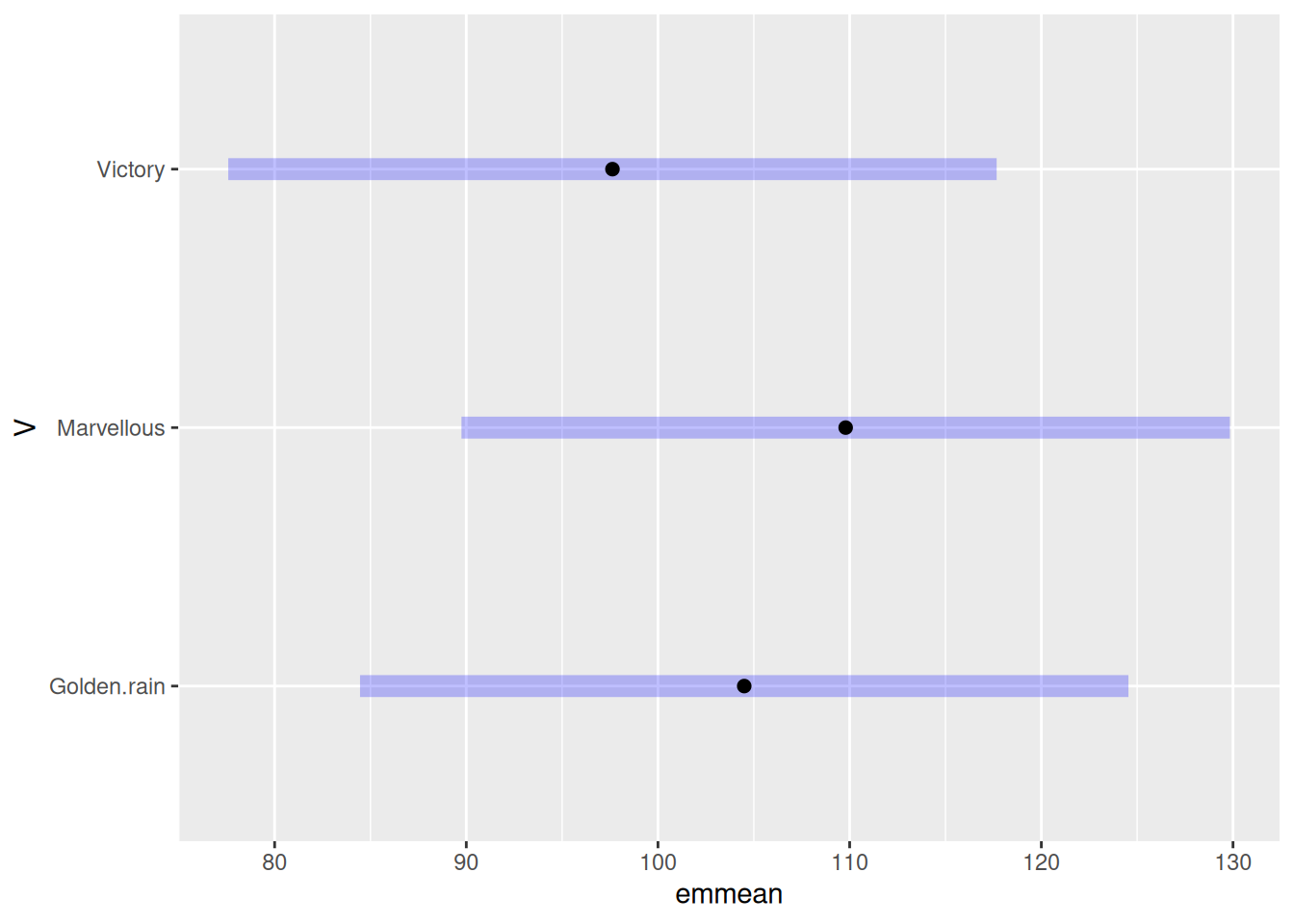
Recall: groups that do not differ significantly from each other share the same letter.
We can also use the emmip() function from the emmeans package to examine the trend in the interaction between variety and nitrogen factors.
emmip(model1, N ~ V)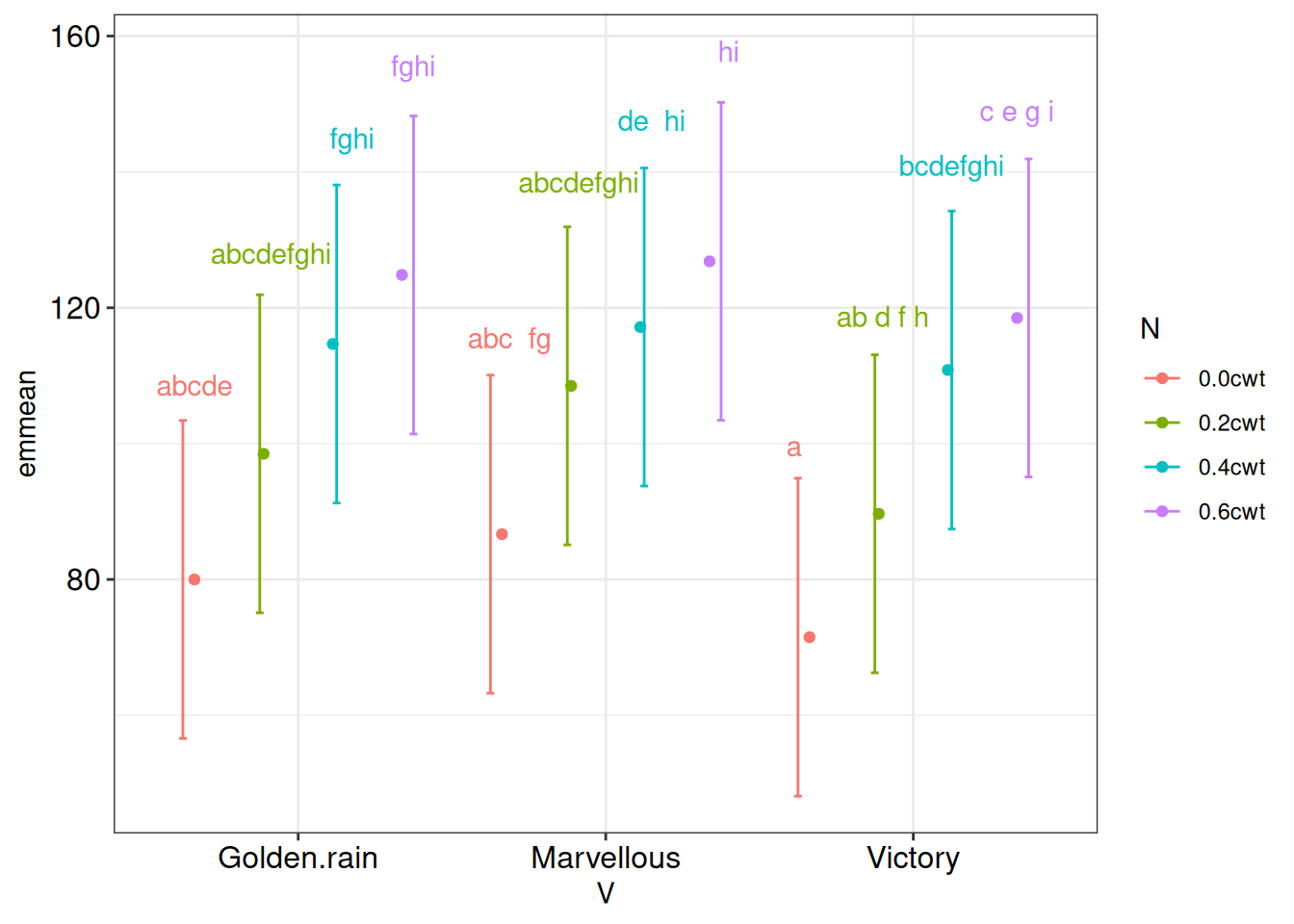
The package emmeans provides extensive functionality for estimating means, confidence intervals, making contrasts and more. To learn more about this functionality, see the vignettes for this package.
13.8 Conclusion
Be cautious with the terms “significant” and “non-significant”, and don’t interpret a “non-significant” result as there is no effect. Follow good statistical practices such as getting the model right first, and using adjusted P-values for appropriately chosen families of comparisons or contrasts.
P values are often misinterpreted, and the term “statistical significance” can be misleading. Please refer to this link to read more about basic principles outlined by the American Statistical Association when considering p-values.