Section 8 Other Models - SAS
8.1 Other Experimental and Treatment Designs
Spatial models can be extended to fit other experimental designs such as CRD, Lattice, and split plot or treatment designs such as factorials.
Below are minimal examples that omit several steps conducted in section 6 (e.g. fitting the empirical variogram) for brevity. Also, although spatial variance is incorporated into each example, we have not made an effort to ensure that each is the best fitting model for the data. The examples are intended to illustrate the correct syntax rather than the complete process of proper model fitting.
Unless indicated otherwise, these data are adapted from the R package agridat. Specific links to csv data files are given in the examples.
8.1.1 Completely randomized design (CRD)
Data: cochran_crd.csv
This study investigated the effect of sulfur on controlling scab disease in potatoes and had seven treatments (trt) measuring the percent surface area infected (inf). Row and column indices are also given. The design was a completely randomized design with 8 control replications and 4 treatment replications.
Two possible methods of adjustment are shown: row column trend adjustment (as suggested in agridat), and a spline adjustment.
ods html close;
proc format;
invalue has_NA
'NA' = .;
run;
filename CRD url "https://raw.githubusercontent.com/IdahoAgStats/guide-to-field-trial-spatial-analysis/master/data/cochran_crd.csv";
data CRD;
infile CRD firstobs=2 delimiter=',';
input inf trt$ row col;
informat inf has_NA.;
if inf=. then delete;
run;
proc mixed data=crd;
class trt;
model inf=trt row col;
run;
proc glimmix data=crd;
class trt;
effect sp_r = spline(row col);
model inf=trt sp_r;
random row col/type=rsmooth;
run;
ods html; 8.1.2 Multi-way Factorials
Data: chinloy_fractionalfactorial.csv
Factorial experiments consider multiple treatments and their combinations. The study here evaluated the effect of 5 different fertilizer treatments (nitrogen, phosphorus, potassium, bagasse, and a filter mud press), each at various concentrations, on sugarcane yield. The levels of {0,1,2} indicate the relative concentrations of each fertilizer. Because all possible treatment combinations were too numerous, only a subset were used (fractional factorial) and only 2-way interactions with nitrogen are evaluated in the model. The treatments were laid out in a randomized complete block design (block).
A Gaussian spatial model is used below.
ods html close;
proc format;
invalue has_NA
'NA' = .;
run;
filename FACT url "https://raw.githubusercontent.com/IdahoAgStats/guide-to-field-trial-spatial-analysis/master/data/chinloy_fractionalfactorial.csv";
data Factorial;
infile FACT firstobs=2 delimiter=',';
input yield block$ row col trt N P K B F;
informat yield has_NA.;
if yield=. then delete;
run;
proc mixed data=Factorial maxiter=150;
class block N P K B F;
model yield = N P K B F N*P N*K N*B N*F/ ddfm=kr;
random block;
repeated/subject=intercept type=sp(gau) (row col) local;
parms (6) (.25) (.21) (.1);
run;
ods html;8.1.3 Alpha lattice
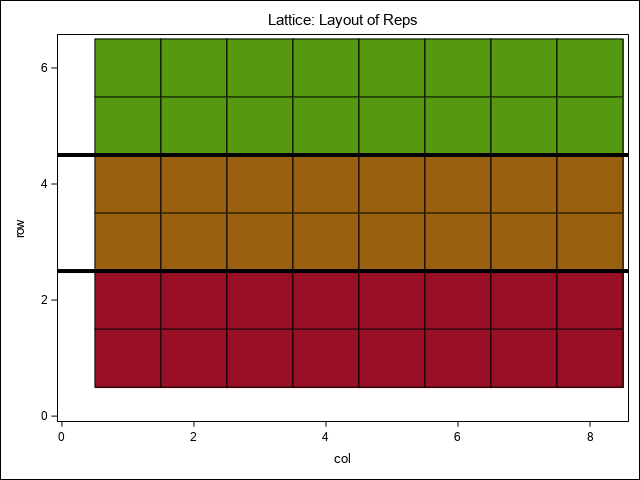
The burgueno.alpha data set is set up as an incomplete block alpha design with 16 treatment levels (gen). There are 12 blocks, 2 each within 3 reps. The code below illustrates the layout of the reps and blocks. Two examples of spatial adjustment are shown: 1) assuming a Gaussian spatial adjustment, and 2) utilizing a spline adjustment.
proc format;
invalue has_NA
'NA' = .;
run;
filename ALPHA url "https://raw.githubusercontent.com/IdahoAgStats/guide-to-field-trial-spatial-analysis/master/data/burgueno_alpha.csv";
data Lattice;
infile ALPHA firstobs=2 delimiter=',';
input rep$ block$ row col gen$ yield;
informat yield has_NA.;
if yield=. then delete;
run;
proc sgplot data=Lattice;
styleattrs datacolors=(cx990F26 cx99600F cx54990F);
HEATMAPPARM y=row x=col COLORgroup=rep/ outline;
refline 2.5 4.5/axis=y LINEATTRS=(color=black thickness=4) ;
title1 'Lattice: Layout of Reps';
run;
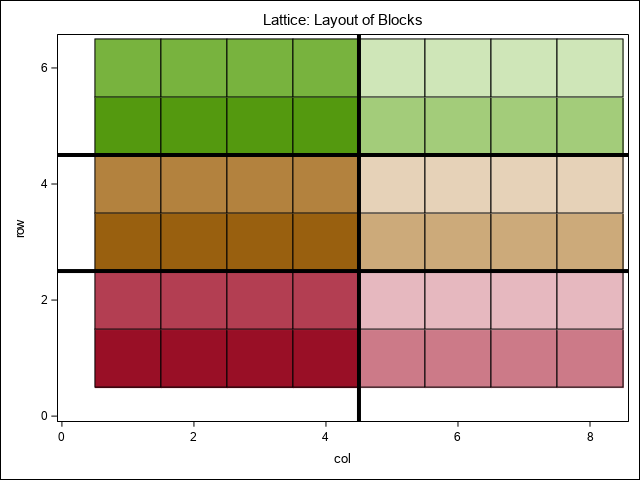
proc sgplot data=Lattice;
styleattrs datacolors=(cx990F26 cxCC7A88 cxB33E52 cxE6B8BF
cx99600F cxCCAA7A cxB3823E cxE6D2B8
cx54990F cxA3CC7A cx78B33E cxCFE6B8);
HEATMAPPARM y=row x=col COLORgroup=block/ outline;
refline 2.5 4.5/axis=y LINEATTRS=(color=black thickness=4) ;
refline 4.5/axis=x LINEATTRS=(color=black thickness=4);
title1 'Lattice: Layout of Blocks';
run;ods html close;
proc mixed data=Lattice ;
class block rep gen;
model yield = gen/ ddfm=kr;
random rep block(rep);
repeated/subject=intercept type=sp(gau) (row col) local;
parms (4)(30711) (57790)(86861) (133229);
run;
proc glimmix data=Lattice ;
class block rep gen;
effect sp_r = spline(row col);
model yield = gen sp_r/ ddfm=kr;
random row col/type=rsmooth;
run;
ods html;8.1.4 Latin square
Latin is a special example of a lattice experiment where each treatment occurs once in each row and in each column. As a result, the row and column effects are used to model spatial effects intrinsically.
The *cochran.latin** data set examines the effect of an 6 “operators” (persons) on the difference between the true plot height and operator-measured shoot height from 6 wheat plots. Each person measured the plots in a different order according to a Latin Square design. While this example is not strictly spatial in nature, it illustrates the setup for analysis.
ods html close;
proc format;
invalue has_NA
'NA' = .;
run;
filename LAT url "https://raw.githubusercontent.com/IdahoAgStats/guide-to-field-trial-spatial-analysis/master/data/cochran_latin.csv";
data Latin;
infile LAT firstobs=2 delimiter=',';
input row col operator$ diff;
informat diff has_NA.;
if diff=. then delete;
run;
proc mixed data=latin;
class row col operator;
model diff = operator;
random row col;
run;
ods html;8.1.5 Split plot
A split plot is a factorial treatment design with a restriction on the randomization of the factors. In this example, the durban.splitplot data looks at the effect of two factors: fungicide and barley varieties. The study is set up with 4 blocks. Within each block, 2 fungicides are randomized as whole or main plots. Within each fungicide treatment, 70 barley varieties are then randomized separately as subplots. The resulting analysis then breaks out separate error terms for the whole plots and the subplots. The plots are arranged into 10 rows x 56 columns (‘beds’). Spatial adjustment can then be introduced on top of this structure, if needed. The examples below illustrate a spherical spatial model adjustment and a spline adjustment.
ods html close;
proc format;
invalue has_NA
'NA' = .;
run;
filename SPLIT url "https://raw.githubusercontent.com/IdahoAgStats/guide-to-field-trial-spatial-analysis/master/data/durban_splitplot.csv";
data splitplot;
infile SPLIT firstobs=2 delimiter=',';
input yield block$ gen$ fung$ row bed;
informat yield has_NA.;
if yield=. then delete;
run;
proc mixed data=splitplot;
class block gen fung row bed;
model yield = fung gen fung*gen/outp=residuals;
random block block*fung;
repeated/subject=intercept type=sp(sph) (row bed) local;
parms (7)(0.03)(0.03)(0.03) (0.01);
run;
proc glimmix data=splitplot;
class block gen fung;
effect sp_r = spline(row bed);
model yield = fung gen fung*gen sp_r;
random block block*fung;
random row bed/type=rsmooth;
run;
ods html;8.1.6 Split-split plot
Like the Split-Plot above, the Split-Split-Plot is a factorial design, this time with an additional restriction on the randomization. The archbold.apple data used here describes the yield of apple trees under the impact of tree spacing (the whole or main plot), tree root stock (the split plot), and tree variety (the split-split plot). That is, 3 tree spacings are randomized in each block. Within those spacings, 4 root stocks are randomized separately, and then within each of those 2 varieties (‘gen’) are randomized. There are 5 blocks (‘rep’) and separate error terms for spacing, root stock, and variety are broken out in the analysis. In addition, we have row and column (‘pos’) information for the plots. This example uses a spline spatial adjustment.
ods html close;
proc format;
invalue has_NA
'NA' = .;
run;
filename SPLIT url "https://raw.githubusercontent.com/IdahoAgStats/guide-to-field-trial-spatial-analysis/master/data/archbold_apple.csv";
data sp_sp_plot;
infile SPLIT firstobs=2 delimiter=',';
input rep$ row pos spacing$ stock$ gen$ yield trt;
informat yield has_NA.;
if yield=. then delete;
run;
proc glimmix data=sp_sp_plot;
class rep spacing stock gen;
effect sp_r = spline(row pos);
model yield = spacing stock spacing*stock gen gen*spacing gen*stock gen*spacing*stock sp_r;
random rep rep*spacing rep*stock*spacing;
random row pos/type=rsmooth;
run;
ods html;8.1.7 Split block or Strip plot
This study (little.splitblock) investigated the effects of nitrogen rates (4 levels) and harvest dates (5 dates) on sugarbeet yields using 4 blocks. Similar to a Latin square, the split block design has two main factors defined in rows and columns. Within each block the rows and columns, each representing one of the factors, are independently randomized. The effect of this in the analysis of variance is to break out separate error terms and DF for each main effect as well as their interaction. In this example the spline spatial adjustment is demonstrated.
ods html close;
proc format;
invalue has_NA
'NA' = .;
run;
filename SPLITB url "https://raw.githubusercontent.com/IdahoAgStats/guide-to-field-trial-spatial-analysis/master/data/little_splitblock.csv";
data sb;
infile SPLITB firstobs=2 delimiter=',';
input row col yield harvest nitro block$;
informat yield has_NA.;
if yield=. then delete;
run;
proc glimmix data=sb;
class harvest nitro block;
effect sp_r = spline(row col);
model yield = harvest nitro harvest*nitro sp_r;
random block harvest*block nitro*block harvest*nitro*block;
random row col/type=rsmooth;
run;
ods html;8.1.8 Augmented design
The augmented experimental design occurs most commonly, if not exclusively, in plant breeding studies. It can be useful when the number of treatments is very large and the primary goal of the study is to rank or select genotypes that perform to a specified level. The number of treatments and/or limited materials often preclude complete replication of all treatments. To adjust for this, only a select set of genotypes, usually of known performance, are replicated in the design. The error estimated from these select genotypes is then utilized in the analysis to evaluate the remaining genotypes. Juan Burgueño (2018) have a very good discussion of this design and analysis of it. The example below uses their ‘P2’ model and the reader is referred to Juan Burgueño (2018) for more details.
The data used here refer to a wheat genotype evaluation study carried out near Lind Washington. The study looked at 922 lines (‘name’), of which, 8 were replicated known varieties. The P2 model, mentioned above, compares the averages of replicated lines to unreplicated lines. The data steps and procedures used below define these groups in an indicator variable named d2. The response variable, ‘yieldg’, is converted to kilograms (‘yieldkg’) to facilitate computations and avoid numeric overflow errors due to large values.
filename AUG url "https://raw.githubusercontent.com/IdahoAgStats/guide-to-field-trial-spatial-analysis/master/data/augmented_lind.csv";
PROC IMPORT OUT= WORK.augmented
DATAFILE= AUG
DBMS=CSV REPLACE;
GETNAMES=YES;
DATAROW=2;
RUN;
data augmented;
set augmented;
if yieldg = 999999 or yieldg=. then delete; /* Remove missing values */
prow=prow*11.7; /*convert row and column indices to feet */
pcol=pcol*5.5;
run;
proc freq noprint data=augmented;
tables name/out=controls;
run;
data controls;
set controls;
if count >1;
run;
proc sort data=controls;
by name;
run;
proc sort data=augmented;
by name;
run;
data augmented;
merge augmented controls;
by name;
if count=. then d2=2; /* Unreplicated */
else d2=1; /* Replicated */
yieldkg=yieldg/1000;
run;
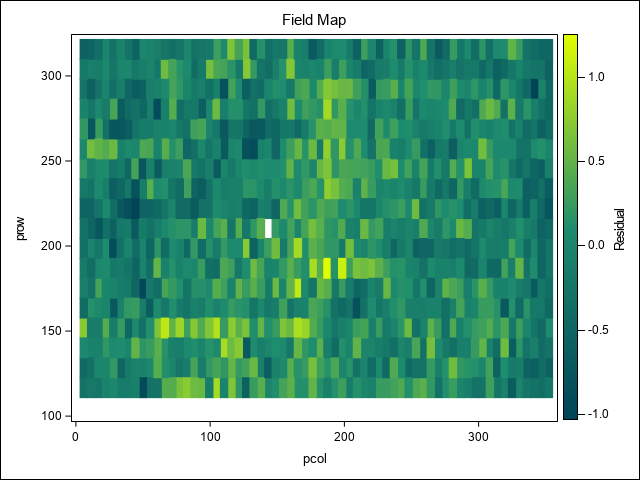
Following the steps described earlier, we first fit a base model, yieldkg = d2, to obtain residuals. We cannot use a base model of yieldkg = name because all the unreplicated lines will produce residual values of 0.
The residuals are then plotted in a heat map. This map shows evidence of spatial patterns and variability across the field.
PROC mixed data=augmented;
class name d2;
model yieldkg = d2/noint outp=residuals ddf=229 229;
lsmeans d2;
*lsmeans name(d2)/slice = d2;
run;
proc sgplot data=residuals;
HEATMAPPARM y=pRow x=pCol COLORRESPONSE=resid/ colormodel=(cx014458 cx1E8C6E cxE1FE01);
title1 'Field Map';
run;| Model Information | |
|---|---|
| Data Set | WORK.AUGMENTED |
| Dependent Variable | yieldkg |
| Covariance Structure | Diagonal |
| Estimation Method | REML |
| Residual Variance Method | Profile |
| Fixed Effects SE Method | Model-Based |
| Degrees of Freedom Method | Residual |
| Class Level Information | ||
|---|---|---|
| Class | Levels | Values |
| name | 922 | 13X0828-0-0-1 13X0828-0-0-102 13X0828-0-0-105 13X0828-0-0-108 13X0828-0-0-109 13X0828-0-0-110 13X0828-0-0-15 13X0828-0-0-17 13X0828-0-0-18 13X0828-0-0-2 13X0828-0-0-24 13X0828-0-0-27 13X0828-0-0-31 13X0828-0-0-33 13X0828-0-0-36 13X0828-0-0-37 13X0828-0-0-40 13X0828-0-0-41 13X0828-0-0-42 13X0828-0-0-48 13X0828-0-0-49 13X0828-0-0-5 13X0828-0-0-52 13X0828-0-0-55 13X0828-0-0-6 13X0828-0-0-61 13X0828-0-0-62 13X0828-0-0-63 13X0828-0-0-66 13X0828-0-0-68 13X0828-0-0-7 13X0828-0-0-80 13X0828-0-0-81 13X0828-0-0-83 13X0828-0-0-9 13X0828-0-0-90 13X0828-0-0-91 13X0828-0-0-92 13X0828-0-0-94 13X0828-0-0-95 13X0828-0-0-97 13X0828-0-0-99 14X1001-0-0-1 14X1001-0-0-105 14X1001-0-0-106 14X1001-0-0-109 14X1001-0-0-11 14X1001-0-0-115 14X1001-0-0-116 14X1001-0-0-119 14X1001-0-0-12 14X1001-0-0-121 14X1001-0-0-122 14X1001-0-0-127 14X1001-0-0-128 14X1001-0-0-13 14X1001-0-0-130 14X1001-0-0-132 14X1001-0-0-134 14X1001-0-0-140 14X1001-0-0-141 14X1001-0-0-144 14X1001-0-0-146 14X1001-0-0-150 14X1001-0-0-156 14X1001-0-0-157 14X1001-0-0-158 14X1001-0-0-16 14X1001-0-0-160 14X1001-0-0-162 14X1001-0-0-164 14X1001-0-0-166 14X1001-0-0-167 14X1001-0-0-168 14X1001-0-0-169 14X1001-0-0-17 14X1001-0-0-174 14X1001-0-0-175 14X1001-0-0-176 14X1001-0-0-177 14X1001-0-0-178 14X1001-0-0-179 14X1001-0-0-181 14X1001-0-0-183 14X1001-0-0-185 14X1001-0-0-188 14X1001-0-0-193 14X1001-0-0-196 14X1001-0-0-197 14X1001-0-0-199 14X1001-0-0-20 14X1001-0-0-200 14X1001-0-0-203 14X1001-0-0-204 14X1001-0-0-205 14X1001-0-0-206 14X1001-0-0-207 14X1001-0-0-208 14X1001-0-0-209 14X1001-0-0-210 14X1001-0-0-211 14X1001-0-0-212 14X1001-0-0-213 14X1001-0-0-214 14X1001-0-0-219 14X1001-0-0-22 14X1001-0-0-223 14X1001-0-0-224 14X1001-0-0-225 14X1001-0-0-24 14X1001-0-0-25 14X1001-0-0-31 14X1001-0-0-33 14X1001-0-0-36 14X1001-0-0-38 14X1001-0-0-4 14X1001-0-0-41 14X1001-0-0-42 14X1001-0-0-43 14X1001-0-0-46 14X1001-0-0-47 14X1001-0-0-48 14X1001-0-0-49 14X1001-0-0-56 14X1001-0-0-57 14X1001-0-0-6 14X1001-0-0-60 14X1001-0-0-61 14X1001-0-0-64 14X1001-0-0-67 14X1001-0-0-68 14X1001-0-0-69 14X1001-0-0-77 14X1001-0-0-8 14X1001-0-0-81 14X1001-0-0-82 14X1001-0-0-87 14X1001-0-0-89 14X1001-0-0-92 14X1001-0-0-93 14X1001-0-0-97 14X1001-0-0-99 14X1003-0-0-1 14X1003-0-0-10 14X1003-0-0-102 14X1003-0-0-105 14X1003-0-0-106 14X1003-0-0-108 14X1003-0-0-110 14X1003-0-0-115 14X1003-0-0-121 14X1003-0-0-122 14X1003-0-0-124 14X1003-0-0-125 14X1003-0-0-127 14X1003-0-0-13 14X1003-0-0-130 14X1003-0-0-133 14X1003-0-0-140 14X1003-0-0-141 14X1003-0-0-146 14X1003-0-0-147 14X1003-0-0-149 14X1003-0-0-16 14X1003-0-0-167 14X1003-0-0-172 14X1003-0-0-175 14X1003-0-0-176 14X1003-0-0-177 14X1003-0-0-178 14X1003-0-0-18 14X1003-0-0-180 14X1003-0-0-181 14X1003-0-0-182 14X1003-0-0-185 14X1003-0-0-186 14X1003-0-0-190 14X1003-0-0-194 14X1003-0-0-195 14X1003-0-0-196 14X1003-0-0-198 14X1003-0-0-2 14X1003-0-0-20 14X1003-0-0-204 14X1003-0-0-21 14X1003-0-0-24 14X1003-0-0-27 14X1003-0-0-28 14X1003-0-0-30 14X1003-0-0-38 14X1003-0-0-41 14X1003-0-0-42 14X1003-0-0-44 14X1003-0-0-46 14X1003-0-0-47 14X1003-0-0-48 14X1003-0-0-49 14X1003-0-0-5 14X1003-0-0-50 14X1003-0-0-51 14X1003-0-0-52 14X1003-0-0-53 14X1003-0-0-54 14X1003-0-0-55 14X1003-0-0-56 14X1003-0-0-6 14X1003-0-0-60 14X1003-0-0-65 14X1003-0-0-66 14X1003-0-0-67 14X1003-0-0-68 14X1003-0-0-70 14X1003-0-0-71 14X1003-0-0-72 14X1003-0-0-73 14X1003-0-0-77 14X1003-0-0-8 14X1003-0-0-83 14X1003-0-0-86 14X1003-0-0-88 14X1003-0-0-92 14X1007-0-0-100 14X1007-0-0-101 14X1007-0-0-104 14X1007-0-0-109 14X1007-0-0-11 14X1007-0-0-111 14X1007-0-0-114 14X1007-0-0-115 14X1007-0-0-120 14X1007-0-0-122 14X1007-0-0-13 14X1007-0-0-16 14X1007-0-0-17 14X1007-0-0-20 14X1007-0-0-21 14X1007-0-0-25 14X1007-0-0-27 14X1007-0-0-29 14X1007-0-0-3 14X1007-0-0-31 14X1007-0-0-33 14X1007-0-0-37 14X1007-0-0-41 14X1007-0-0-47 14X1007-0-0-5 14X1007-0-0-50 14X1007-0-0-53 14X1007-0-0-54 14X1007-0-0-55 14X1007-0-0-59 14X1007-0-0-6 14X1007-0-0-61 14X1007-0-0-65 14X1007-0-0-68 14X1007-0-0-71 14X1007-0-0-72 14X1007-0-0-74 14X1007-0-0-77 14X1007-0-0-79 14X1007-0-0-86 14X1007-0-0-88 14X1007-0-0-9 14X1007-0-0-90 14X1007-0-0-91 14X1007-0-0-92 14X1007-0-0-94 14X1007-0-0-96 14X1007-0-0-98 14X1008-0-0-1 14X1008-0-0-10 14X1008-0-0-11 14X1008-0-0-14 14X1008-0-0-17 14X1008-0-0-2 14X1008-0-0-21 14X1008-0-0-22 14X1008-0-0-26 14X1008-0-0-28 14X1008-0-0-32 14X1008-0-0-33 14X1008-0-0-34 14X1008-0-0-4 14X1008-0-0-40 14X1008-0-0-42 14X1008-0-0-45 14X1008-0-0-46 14X1008-0-0-47 14X1008-0-0-48 14X1008-0-0-49 14X1008-0-0-5 14X1008-0-0-50 14X1008-0-0-54 14X1008-0-0-6 14X1008-0-0-61 14X1008-0-0-65 14X1008-0-0-7 14X1008-0-0-77 14X1008-0-0-78 14X1008-0-0-8 14X1008-0-0-82 14X1008-0-0-83 14X1008-0-0-85 14X1008-0-0-9 14X1022-0-0-12 14X1022-0-0-16 14X1022-0-0-2 14X1022-0-0-39 14X1022-0-0-43 14X1022-0-0-46 14X1022-0-0-49 14X1022-0-0-52 14X1022-0-0-53 14X1022-0-0-56 14X1022-0-0-59 14X1022-0-0-60 14X1022-0-0-61 14X1022-0-0-64 14X1022-0-0-66 14X1022-0-0-68 14X1022-0-0-70 14X1022-0-0-72 14X1022-0-0-76 14X1022-0-0-78 14X1023-0-0-18 14X1023-0-0-30 14X1023-0-0-33 14X1023-0-0-38 14X1023-0-0-39 14X1023-0-0-4 14X1023-0-0-45 14X1023-0-0-48 14X1023-0-0-49 14X1023-0-0-59 14X1023-0-0-70 14X1023-0-0-71 14X1023-0-0-73 14X1023-0-0-74 14X1023-0-0-75 14X1023-0-0-76 14X1023-0-0-78 14X1023-0-0-79 14X1023-0-0-80 14X1023-0-0-82 14X1023-0-0-85 14X1023-0-0-89 14X1023-0-0-90 14X1023-0-0-91 14X1027-0-0-104 14X1027-0-0-107 14X1027-0-0-11 14X1027-0-0-110 14X1027-0-0-112 14X1027-0-0-117 14X1027-0-0-121 14X1027-0-0-122 14X1027-0-0-123 14X1027-0-0-126 14X1027-0-0-128 14X1027-0-0-17 14X1027-0-0-22 14X1027-0-0-23 14X1027-0-0-25 14X1027-0-0-36 14X1027-0-0-37 14X1027-0-0-39 14X1027-0-0-4 14X1027-0-0-40 14X1027-0-0-43 14X1027-0-0-44 14X1027-0-0-45 14X1027-0-0-59 14X1027-0-0-62 14X1027-0-0-70 14X1027-0-0-77 14X1027-0-0-8 14X1027-0-0-82 14X1027-0-0-85 14X1027-0-0-92 14X1027-0-0-94 14X1030-0-0-1 14X1030-0-0-111 14X1030-0-0-112 14X1030-0-0-113 14X1030-0-0-120 14X1030-0-0-123 14X1030-0-0-128 14X1030-0-0-13 14X1030-0-0-131 14X1030-0-0-135 14X1030-0-0-14 14X1030-0-0-141 14X1030-0-0-145 14X1030-0-0-149 14X1030-0-0-16 14X1030-0-0-160 14X1030-0-0-161 14X1030-0-0-164 14X1030-0-0-168 14X1030-0-0-17 14X1030-0-0-176 14X1030-0-0-177 14X1030-0-0-18 14X1030-0-0-185 14X1030-0-0-188 14X1030-0-0-2 14X1030-0-0-215 14X1030-0-0-216 14X1030-0-0-220 14X1030-0-0-222 14X1030-0-0-226 14X1030-0-0-228 14X1030-0-0-25 14X1030-0-0-29 14X1030-0-0-36 14X1030-0-0-40 14X1030-0-0-54 14X1030-0-0-55 14X1030-0-0-68 14X1030-0-0-71 14X1030-0-0-72 14X1030-0-0-76 14X1030-0-0-77 14X1030-0-0-78 14X1030-0-0-80 14X1030-0-0-81 14X1030-0-0-84 14X1030-0-0-88 14X1030-0-0-93 14X1030-0-0-97 14X1031-0-0-105 14X1031-0-0-110 14X1031-0-0-112 14X1031-0-0-113 14X1031-0-0-114 14X1031-0-0-117 14X1031-0-0-120 14X1031-0-0-121 14X1031-0-0-125 14X1031-0-0-134 14X1031-0-0-136 14X1031-0-0-14 14X1031-0-0-141 14X1031-0-0-143 14X1031-0-0-147 14X1031-0-0-149 14X1031-0-0-16 14X1031-0-0-160 14X1031-0-0-161 14X1031-0-0-18 14X1031-0-0-2 14X1031-0-0-20 14X1031-0-0-21 14X1031-0-0-22 14X1031-0-0-23 14X1031-0-0-24 14X1031-0-0-28 14X1031-0-0-29 14X1031-0-0-3 14X1031-0-0-30 14X1031-0-0-32 14X1031-0-0-34 14X1031-0-0-35 14X1031-0-0-36 14X1031-0-0-4 14X1031-0-0-51 14X1031-0-0-52 14X1031-0-0-59 14X1031-0-0-6 14X1031-0-0-60 14X1031-0-0-64 14X1031-0-0-90 14X1031-0-0-93 14X1031-0-0-94 14X1031-0-0-96 14X1053-0-0-10 14X1053-0-0-103 14X1053-0-0-106 14X1053-0-0-107 14X1053-0-0-109 14X1053-0-0-110 14X1053-0-0-111 14X1053-0-0-118 14X1053-0-0-120 14X1053-0-0-124 14X1053-0-0-128 14X1053-0-0-13 14X1053-0-0-130 14X1053-0-0-131 14X1053-0-0-132 14X1053-0-0-133 14X1053-0-0-136 14X1053-0-0-137 14X1053-0-0-138 14X1053-0-0-139 14X1053-0-0-14 14X1053-0-0-142 14X1053-0-0-143 14X1053-0-0-146 14X1053-0-0-147 14X1053-0-0-149 14X1053-0-0-15 14X1053-0-0-151 14X1053-0-0-153 14X1053-0-0-154 14X1053-0-0-155 14X1053-0-0-157 14X1053-0-0-158 14X1053-0-0-162 14X1053-0-0-164 14X1053-0-0-166 14X1053-0-0-167 14X1053-0-0-168 14X1053-0-0-169 14X1053-0-0-170 14X1053-0-0-172 14X1053-0-0-174 14X1053-0-0-179 14X1053-0-0-180 14X1053-0-0-182 14X1053-0-0-19 14X1053-0-0-20 14X1053-0-0-23 14X1053-0-0-28 14X1053-0-0-29 14X1053-0-0-31 14X1053-0-0-33 14X1053-0-0-37 14X1053-0-0-4 14X1053-0-0-47 14X1053-0-0-5 14X1053-0-0-51 14X1053-0-0-52 14X1053-0-0-54 14X1053-0-0-55 14X1053-0-0-56 14X1053-0-0-58 14X1053-0-0-59 14X1053-0-0-6 14X1053-0-0-61 14X1053-0-0-63 14X1053-0-0-65 14X1053-0-0-66 14X1053-0-0-7 14X1053-0-0-71 14X1053-0-0-73 14X1053-0-0-74 14X1053-0-0-75 14X1053-0-0-76 14X1053-0-0-77 14X1053-0-0-78 14X1053-0-0-80 14X1053-0-0-81 14X1053-0-0-82 14X1053-0-0-87 14X1053-0-0-89 14X1053-0-0-9 14X1053-0-0-91 14X1053-0-0-92 14X1053-0-0-93 14X1053-0-0-97 14X1053-0-0-98 14X1054-0-0-1 14X1054-0-0-10 14X1054-0-0-14 14X1054-0-0-18 14X1054-0-0-2 14X1054-0-0-27 14X1054-0-0-28 14X1054-0-0-3 14X1054-0-0-31 14X1054-0-0-32 14X1054-0-0-34 14X1054-0-0-46 14X1054-0-0-5 14X1054-0-0-55 14X1054-0-0-6 14X1054-0-0-60 14X1054-0-0-61 14X1054-0-0-62 14X1054-0-0-64 14X1054-0-0-65 14X1054-0-0-9 14X1082-0-0-10 14X1082-0-0-12 14X1082-0-0-19 14X1082-0-0-20 14X1082-0-0-21 14X1082-0-0-22 14X1082-0-0-25 14X1082-0-0-27 14X1082-0-0-34 14X1082-0-0-7 14X1083-0-0-10 14X1083-0-0-100 14X1083-0-0-103 14X1083-0-0-104 14X1083-0-0-108 14X1083-0-0-112 14X1083-0-0-118 14X1083-0-0-12 14X1083-0-0-120 14X1083-0-0-129 14X1083-0-0-130 14X1083-0-0-134 14X1083-0-0-14 14X1083-0-0-140 14X1083-0-0-142 14X1083-0-0-146 14X1083-0-0-15 14X1083-0-0-157 14X1083-0-0-161 14X1083-0-0-162 14X1083-0-0-166 14X1083-0-0-167 14X1083-0-0-168 14X1083-0-0-174 14X1083-0-0-18 14X1083-0-0-183 14X1083-0-0-188 14X1083-0-0-191 14X1083-0-0-192 14X1083-0-0-197 14X1083-0-0-205 14X1083-0-0-213 14X1083-0-0-218 14X1083-0-0-221 14X1083-0-0-223 14X1083-0-0-230 14X1083-0-0-231 14X1083-0-0-234 14X1083-0-0-235 14X1083-0-0-238 14X1083-0-0-24 14X1083-0-0-243 14X1083-0-0-245 14X1083-0-0-251 14X1083-0-0-254 14X1083-0-0-256 14X1083-0-0-26 14X1083-0-0-260 14X1083-0-0-268 14X1083-0-0-3 14X1083-0-0-30 14X1083-0-0-33 14X1083-0-0-4 14X1083-0-0-46 14X1083-0-0-54 14X1083-0-0-59 14X1083-0-0-63 14X1083-0-0-65 14X1083-0-0-67 14X1083-0-0-71 14X1083-0-0-72 14X1083-0-0-76 14X1083-0-0-8 14X1083-0-0-86 14X1083-0-0-88 14X1083-0-0-9 14X1083-0-0-91 14X1083-0-0-93 14X1083-0-0-96 14X1083-0-0-99 14X1085-0-0-10 14X1085-0-0-11 14X1085-0-0-27 14X1085-0-0-34 14X1085-0-0-36 14X1085-0-0-56 14X1085-0-0-58 14X1085-0-0-59 14X1085-0-0-68 14X1085-0-0-71 14X1085-0-0-8 14X1085-0-0-83 14X1085-0-0-90 14X1085-0-0-93 14X1085-0-0-96 14X1098-0-0-10 14X1098-0-0-106 14X1098-0-0-109 14X1098-0-0-18 14X1098-0-0-30 14X1098-0-0-31 14X1098-0-0-34 14X1098-0-0-38 14X1098-0-0-39 14X1098-0-0-4 14X1098-0-0-41 14X1098-0-0-46 14X1098-0-0-48 14X1098-0-0-53 14X1098-0-0-54 14X1098-0-0-57 14X1098-0-0-7 14X1098-0-0-70 14X1098-0-0-72 14X1098-0-0-73 14X1098-0-0-79 14X1098-0-0-8 14X1098-0-0-81 14X1098-0-0-83 14X1098-0-0-94 14X1098-0-0-95 14X1098-0-0-96 14X1098-0-0-98 14X1103-0-0-104 14X1103-0-0-105 14X1103-0-0-106 14X1103-0-0-114 14X1103-0-0-115 14X1103-0-0-116 14X1103-0-0-117 14X1103-0-0-12 14X1103-0-0-120 14X1103-0-0-122 14X1103-0-0-124 14X1103-0-0-130 14X1103-0-0-131 14X1103-0-0-135 14X1103-0-0-136 14X1103-0-0-138 14X1103-0-0-141 14X1103-0-0-143 14X1103-0-0-146 14X1103-0-0-147 14X1103-0-0-148 14X1103-0-0-150 14X1103-0-0-155 14X1103-0-0-157 14X1103-0-0-159 14X1103-0-0-16 14X1103-0-0-162 14X1103-0-0-18 14X1103-0-0-27 14X1103-0-0-3 14X1103-0-0-31 14X1103-0-0-33 14X1103-0-0-37 14X1103-0-0-41 14X1103-0-0-42 14X1103-0-0-50 14X1103-0-0-51 14X1103-0-0-56 14X1103-0-0-58 14X1103-0-0-6 14X1103-0-0-63 14X1103-0-0-64 14X1103-0-0-68 14X1103-0-0-75 14X1103-0-0-76 14X1103-0-0-77 14X1103-0-0-79 14X1103-0-0-8 14X1103-0-0-80 14X1103-0-0-81 14X1103-0-0-83 14X1103-0-0-91 14X1103-0-0-96 14X1114-0-0-1 14X1114-0-0-101 14X1114-0-0-104 14X1114-0-0-105 14X1114-0-0-18 14X1114-0-0-23 14X1114-0-0-25 14X1114-0-0-26 14X1114-0-0-32 14X1114-0-0-36 14X1114-0-0-37 14X1114-0-0-4 14X1114-0-0-45 14X1114-0-0-48 14X1114-0-0-54 14X1114-0-0-60 14X1114-0-0-62 14X1114-0-0-64 14X1114-0-0-7 14X1114-0-0-73 14X1114-0-0-75 14X1114-0-0-79 14X1114-0-0-80 14X1114-0-0-84 14X1114-0-0-85 14X1114-0-0-90 14X1114-0-0-91 14X1114-0-0-92 14X1114-0-0-93 14X1114-0-0-97 14X1115-0-0-11 14X1115-0-0-14 14X1115-0-0-17 14X1115-0-0-2 14X1115-0-0-20 14X1115-0-0-21 14X1115-0-0-22 14X1115-0-0-25 14X1115-0-0-26 14X1115-0-0-28 14X1115-0-0-29 14X1115-0-0-31 14X1115-0-0-37 14X1115-0-0-41 14X1115-0-0-45 14X1115-0-0-48 14X1115-0-0-49 14X1115-0-0-5 14X1115-0-0-50 14X1115-0-0-51 14X1115-0-0-52 14X1115-0-0-53 14X1115-0-0-55 14X1115-0-0-56 14X1115-0-0-58 14X1115-0-0-6 14X1115-0-0-60 14X1115-0-0-62 14X1115-0-0-64 14X1115-0-0-66 14X1115-0-0-68 14X1115-0-0-69 14X1115-0-0-7 14X1115-0-0-73 14X1115-0-0-74 14X1115-0-0-77 14X1117-0-0-104 14X1117-0-0-114 14X1117-0-0-117 14X1117-0-0-12 14X1117-0-0-14 14X1117-0-0-23 14X1117-0-0-24 14X1117-0-0-26 14X1117-0-0-29 14X1117-0-0-3 14X1117-0-0-35 14X1117-0-0-36 14X1117-0-0-37 14X1117-0-0-38 14X1117-0-0-4 14X1117-0-0-43 14X1117-0-0-45 14X1117-0-0-46 14X1117-0-0-49 14X1117-0-0-50 14X1117-0-0-55 14X1117-0-0-6 14X1117-0-0-61 14X1117-0-0-64 14X1117-0-0-67 14X1117-0-0-69 14X1117-0-0-70 14X1117-0-0-72 14X1117-0-0-73 14X1117-0-0-74 14X1117-0-0-79 14X1117-0-0-8 14X1117-0-0-82 14X1117-0-0-83 14X1117-0-0-84 14X1117-0-0-85 14X1117-0-0-89 14X1117-0-0-9 14X1117-0-0-90 14X1117-0-0-92 14X1117-0-0-94 14X1117-0-0-96 14X1117-0-0-98 14X1117-0-0-99 14X1118-0-0-11 14X1118-0-0-119 14X1118-0-0-139 14X1118-0-0-14 14X1118-0-0-142 14X1118-0-0-15 14X1118-0-0-17 14X1118-0-0-173 14X1118-0-0-174 14X1118-0-0-178 14X1118-0-0-18 14X1118-0-0-188 14X1118-0-0-190 14X1118-0-0-194 14X1118-0-0-196 14X1118-0-0-198 14X1118-0-0-199 14X1118-0-0-20 14X1118-0-0-204 14X1118-0-0-208 14X1118-0-0-21 14X1118-0-0-22 14X1118-0-0-226 14X1118-0-0-23 14X1118-0-0-24 14X1118-0-0-26 14X1118-0-0-28 14X1118-0-0-32 14X1118-0-0-34 14X1118-0-0-35 14X1118-0-0-36 14X1118-0-0-37 14X1118-0-0-42 14X1118-0-0-43 14X1118-0-0-48 14X1118-0-0-50 14X1118-0-0-51 14X1118-0-0-52 14X1118-0-0-6 14X1118-0-0-64 14X1118-0-0-72 14X1118-0-0-92 14X1118-0-0-95 14X1118-0-0-99 ARS Crescent BRUEHL Bobtail Jasper LCS-HULK Otto Pritchett SY Banks SY Command |
| d2 | 2 | 1 2 |
| Dimensions | |
|---|---|
| Covariance Parameters | 1 |
| Columns in X | 2 |
| Columns in Z | 0 |
| Subjects | 1 |
| Max Obs per Subject | 1151 |
| Number of Observations | |
|---|---|
| Number of Observations Read | 1151 |
| Number of Observations Used | 1151 |
| Number of Observations Not Used | 0 |
| Covariance Parameter Estimates | |
|---|---|
| Cov Parm | Estimate |
| Residual | 0.1200 |
| Fit Statistics | |
|---|---|
| -2 Res Log Likelihood | 836.8 |
| AIC (Smaller is Better) | 838.8 |
| AICC (Smaller is Better) | 838.8 |
| BIC (Smaller is Better) | 843.8 |
| Type 3 Tests of Fixed Effects | ||||
|---|---|---|---|---|
| Effect | Num DF | Den DF | F Value | Pr > F |
| d2 | 2 | 229 | 20749.8 | <.0001 |
| Least Squares Means | ||||||
|---|---|---|---|---|---|---|
| Effect | d2 | Estimate |
Standard Error |
DF | t Value | Pr > |t| |
| d2 | 1 | 2.2018 | 0.02245 | 229 | 98.06 | <.0001 |
| d2 | 2 | 2.0471 | 0.01146 | 229 | 178.56 | <.0001 |
The spatial variability evident in the residuals is then modeled as before. Only one model, power, is applicable to this data.
/*
proc variogram data=residuals plots=pairs(thr=50) ;
compute novariogram nhclasses=60;
coordinates xc=prow yc=pcol;
var resid;
run;
proc variogram data=residuals plots(only)=(semivar);
compute lagd=6.6 maxlags=20;
coordinates xc=prow yc=pcol;
var resid;
run;
*/
proc variogram data=residuals plots(only)=(fitplot);
where yieldkg ^= .;
coordinates xc=pcol yc=pRow;
compute lagd=6.6 maxlags=25;
model form=auto(mlist=(gau, exp, pow, sph) nest=1);
var resid;
run;
| Number of Observations Read | 1151 |
|---|---|
| Number of Observations Used | 1151 |
| Empirical Semivariogram | |||
|---|---|---|---|
|
Lag Class |
Pair Count |
Average Distance |
Semivariance |
| 0 | 0 | . | . |
| 1 | 1132 | 5.5 | 0.074 |
| 2 | 6442 | 13.4 | 0.091 |
| 3 | 4244 | 19.7 | 0.094 |
| 4 | 10058 | 25.8 | 0.101 |
| 5 | 11656 | 33.7 | 0.105 |
| 6 | 10288 | 39.4 | 0.105 |
| 7 | 12614 | 46.2 | 0.106 |
| 8 | 14102 | 51.9 | 0.110 |
| 9 | 20050 | 59.4 | 0.109 |
| 10 | 12140 | 65.9 | 0.114 |
| 11 | 21580 | 72.2 | 0.113 |
| 12 | 16310 | 79.2 | 0.115 |
| 13 | 21474 | 85.3 | 0.117 |
| 14 | 21548 | 92.8 | 0.117 |
| 15 | 20140 | 99.1 | 0.120 |
| 16 | 21671 | 106.1 | 0.118 |
| 17 | 18706 | 112.2 | 0.123 |
| 18 | 25052 | 118.9 | 0.122 |
| 19 | 18018 | 125.8 | 0.126 |
| 20 | 23362 | 131.9 | 0.126 |
| 21 | 19610 | 138.9 | 0.127 |
| 22 | 19241 | 144.7 | 0.131 |
| 23 | 22594 | 151.6 | 0.132 |
| 24 | 19995 | 158.3 | 0.136 |
| 25 | 18681 | 164.9 | 0.132 |
| Semivariogram Model Fitting | |
|---|---|
| Model | Selection from 4 form combinations |
| Fit Summary | ||||
|---|---|---|---|---|
| Class | Model |
Weighted SSE |
AIC | Notes |
| 1 | Pow | 55.66695 | 26.01277 | |
| Exp | 70.00313 | 31.74160 | ||
| Sph | 77.47353 | 34.27651 | Questionable fit | |
| Gau | 119.27905 | 45.06475 | ||
|
Semivariogram Model Fitting |
|
|---|---|
| Name | Power |
| Label | Pow |
| Model Information | |
|---|---|
| Parameter |
Initial Value |
| Nugget | 0.0628 |
| Slope | 0.000443 |
| Expon | 0.5000 |
| Optimization Information | |
|---|---|
| Optimization Technique | Dual Quasi-Newton |
| Parameters in Optimization | 3 |
| Lower Boundaries | 3 |
| Upper Boundaries | 1 |
| Starting Values From | PROC |
| Parameter Estimates | ||||||
|---|---|---|---|---|---|---|
| Parameter | Estimate |
Approx Std Error |
DF | t Value |
Approx Pr > |t| |
Gradient |
| Nugget | 0.07429 | 0.000554 | 22 | 134.20 | <.0001 | -0.10262 |
| Slope | 0.005178 | 0 | 22 | . | . | -0.74912 |
| Expon | 0.4748 | 0.002680 | 22 | 177.15 | <.0001 | -0.01655 |
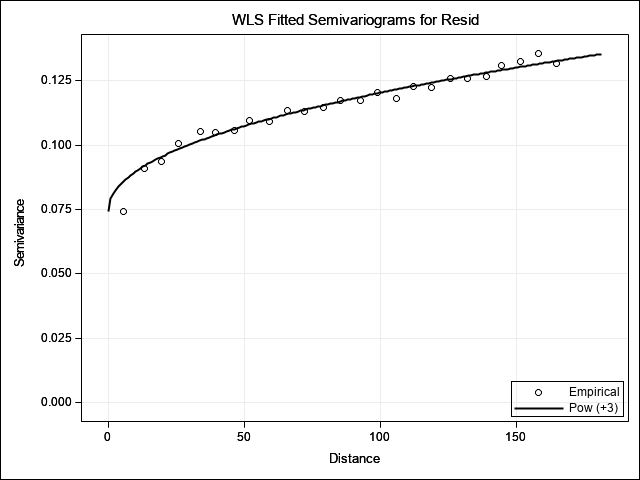
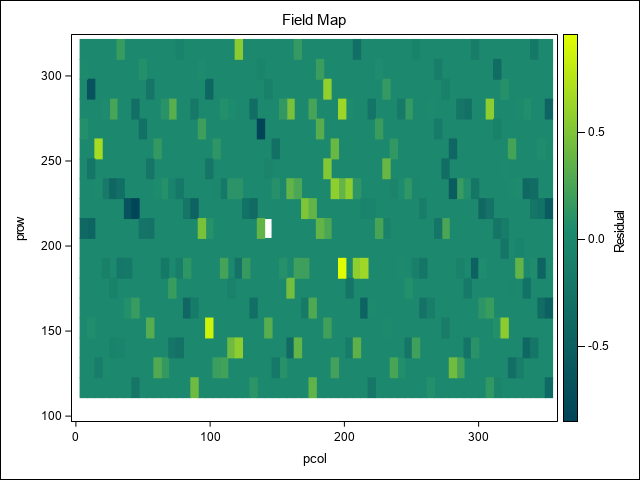
Using the variogram model parameters estimated above, an adjusted model is then fit to the P2 hypothesis of Juan Burgueño (2018). The residuals from this model show little, if any, spatial variability remains after adjustment.
Note: the lsmeans statement is commented out in this example to avoid a large amount of output.
PROC mixed data=augmented;
class name d2;
model yieldkg = d2 name(d2)/outp=adjresiduals ddf=229 229;
lsmeans d2;
repeated/subject=intercept type=sp(pow)(prow pcol) local;
ods output SolutionR =parms;
parms (0.074) (0.0051)(0.475) ;
*lsmeans name(d2)/slice = d2;
run;
proc sgplot data=adjresiduals;
HEATMAPPARM y=pRow x=pCol COLORRESPONSE=resid/ colormodel=(cx014458 cx1E8C6E cxE1FE01);
title1 'Field Map';
run;| Model Information | |
|---|---|
| Data Set | WORK.AUGMENTED |
| Dependent Variable | yieldkg |
| Covariance Structure | Spatial Power |
| Subject Effect | Intercept |
| Estimation Method | REML |
| Residual Variance Method | Profile |
| Fixed Effects SE Method | Model-Based |
| Degrees of Freedom Method | Between-Within |
| Class Level Information | ||
|---|---|---|
| Class | Levels | Values |
| name | 922 | 13X0828-0-0-1 13X0828-0-0-102 13X0828-0-0-105 13X0828-0-0-108 13X0828-0-0-109 13X0828-0-0-110 13X0828-0-0-15 13X0828-0-0-17 13X0828-0-0-18 13X0828-0-0-2 13X0828-0-0-24 13X0828-0-0-27 13X0828-0-0-31 13X0828-0-0-33 13X0828-0-0-36 13X0828-0-0-37 13X0828-0-0-40 13X0828-0-0-41 13X0828-0-0-42 13X0828-0-0-48 13X0828-0-0-49 13X0828-0-0-5 13X0828-0-0-52 13X0828-0-0-55 13X0828-0-0-6 13X0828-0-0-61 13X0828-0-0-62 13X0828-0-0-63 13X0828-0-0-66 13X0828-0-0-68 13X0828-0-0-7 13X0828-0-0-80 13X0828-0-0-81 13X0828-0-0-83 13X0828-0-0-9 13X0828-0-0-90 13X0828-0-0-91 13X0828-0-0-92 13X0828-0-0-94 13X0828-0-0-95 13X0828-0-0-97 13X0828-0-0-99 14X1001-0-0-1 14X1001-0-0-105 14X1001-0-0-106 14X1001-0-0-109 14X1001-0-0-11 14X1001-0-0-115 14X1001-0-0-116 14X1001-0-0-119 14X1001-0-0-12 14X1001-0-0-121 14X1001-0-0-122 14X1001-0-0-127 14X1001-0-0-128 14X1001-0-0-13 14X1001-0-0-130 14X1001-0-0-132 14X1001-0-0-134 14X1001-0-0-140 14X1001-0-0-141 14X1001-0-0-144 14X1001-0-0-146 14X1001-0-0-150 14X1001-0-0-156 14X1001-0-0-157 14X1001-0-0-158 14X1001-0-0-16 14X1001-0-0-160 14X1001-0-0-162 14X1001-0-0-164 14X1001-0-0-166 14X1001-0-0-167 14X1001-0-0-168 14X1001-0-0-169 14X1001-0-0-17 14X1001-0-0-174 14X1001-0-0-175 14X1001-0-0-176 14X1001-0-0-177 14X1001-0-0-178 14X1001-0-0-179 14X1001-0-0-181 14X1001-0-0-183 14X1001-0-0-185 14X1001-0-0-188 14X1001-0-0-193 14X1001-0-0-196 14X1001-0-0-197 14X1001-0-0-199 14X1001-0-0-20 14X1001-0-0-200 14X1001-0-0-203 14X1001-0-0-204 14X1001-0-0-205 14X1001-0-0-206 14X1001-0-0-207 14X1001-0-0-208 14X1001-0-0-209 14X1001-0-0-210 14X1001-0-0-211 14X1001-0-0-212 14X1001-0-0-213 14X1001-0-0-214 14X1001-0-0-219 14X1001-0-0-22 14X1001-0-0-223 14X1001-0-0-224 14X1001-0-0-225 14X1001-0-0-24 14X1001-0-0-25 14X1001-0-0-31 14X1001-0-0-33 14X1001-0-0-36 14X1001-0-0-38 14X1001-0-0-4 14X1001-0-0-41 14X1001-0-0-42 14X1001-0-0-43 14X1001-0-0-46 14X1001-0-0-47 14X1001-0-0-48 14X1001-0-0-49 14X1001-0-0-56 14X1001-0-0-57 14X1001-0-0-6 14X1001-0-0-60 14X1001-0-0-61 14X1001-0-0-64 14X1001-0-0-67 14X1001-0-0-68 14X1001-0-0-69 14X1001-0-0-77 14X1001-0-0-8 14X1001-0-0-81 14X1001-0-0-82 14X1001-0-0-87 14X1001-0-0-89 14X1001-0-0-92 14X1001-0-0-93 14X1001-0-0-97 14X1001-0-0-99 14X1003-0-0-1 14X1003-0-0-10 14X1003-0-0-102 14X1003-0-0-105 14X1003-0-0-106 14X1003-0-0-108 14X1003-0-0-110 14X1003-0-0-115 14X1003-0-0-121 14X1003-0-0-122 14X1003-0-0-124 14X1003-0-0-125 14X1003-0-0-127 14X1003-0-0-13 14X1003-0-0-130 14X1003-0-0-133 14X1003-0-0-140 14X1003-0-0-141 14X1003-0-0-146 14X1003-0-0-147 14X1003-0-0-149 14X1003-0-0-16 14X1003-0-0-167 14X1003-0-0-172 14X1003-0-0-175 14X1003-0-0-176 14X1003-0-0-177 14X1003-0-0-178 14X1003-0-0-18 14X1003-0-0-180 14X1003-0-0-181 14X1003-0-0-182 14X1003-0-0-185 14X1003-0-0-186 14X1003-0-0-190 14X1003-0-0-194 14X1003-0-0-195 14X1003-0-0-196 14X1003-0-0-198 14X1003-0-0-2 14X1003-0-0-20 14X1003-0-0-204 14X1003-0-0-21 14X1003-0-0-24 14X1003-0-0-27 14X1003-0-0-28 14X1003-0-0-30 14X1003-0-0-38 14X1003-0-0-41 14X1003-0-0-42 14X1003-0-0-44 14X1003-0-0-46 14X1003-0-0-47 14X1003-0-0-48 14X1003-0-0-49 14X1003-0-0-5 14X1003-0-0-50 14X1003-0-0-51 14X1003-0-0-52 14X1003-0-0-53 14X1003-0-0-54 14X1003-0-0-55 14X1003-0-0-56 14X1003-0-0-6 14X1003-0-0-60 14X1003-0-0-65 14X1003-0-0-66 14X1003-0-0-67 14X1003-0-0-68 14X1003-0-0-70 14X1003-0-0-71 14X1003-0-0-72 14X1003-0-0-73 14X1003-0-0-77 14X1003-0-0-8 14X1003-0-0-83 14X1003-0-0-86 14X1003-0-0-88 14X1003-0-0-92 14X1007-0-0-100 14X1007-0-0-101 14X1007-0-0-104 14X1007-0-0-109 14X1007-0-0-11 14X1007-0-0-111 14X1007-0-0-114 14X1007-0-0-115 14X1007-0-0-120 14X1007-0-0-122 14X1007-0-0-13 14X1007-0-0-16 14X1007-0-0-17 14X1007-0-0-20 14X1007-0-0-21 14X1007-0-0-25 14X1007-0-0-27 14X1007-0-0-29 14X1007-0-0-3 14X1007-0-0-31 14X1007-0-0-33 14X1007-0-0-37 14X1007-0-0-41 14X1007-0-0-47 14X1007-0-0-5 14X1007-0-0-50 14X1007-0-0-53 14X1007-0-0-54 14X1007-0-0-55 14X1007-0-0-59 14X1007-0-0-6 14X1007-0-0-61 14X1007-0-0-65 14X1007-0-0-68 14X1007-0-0-71 14X1007-0-0-72 14X1007-0-0-74 14X1007-0-0-77 14X1007-0-0-79 14X1007-0-0-86 14X1007-0-0-88 14X1007-0-0-9 14X1007-0-0-90 14X1007-0-0-91 14X1007-0-0-92 14X1007-0-0-94 14X1007-0-0-96 14X1007-0-0-98 14X1008-0-0-1 14X1008-0-0-10 14X1008-0-0-11 14X1008-0-0-14 14X1008-0-0-17 14X1008-0-0-2 14X1008-0-0-21 14X1008-0-0-22 14X1008-0-0-26 14X1008-0-0-28 14X1008-0-0-32 14X1008-0-0-33 14X1008-0-0-34 14X1008-0-0-4 14X1008-0-0-40 14X1008-0-0-42 14X1008-0-0-45 14X1008-0-0-46 14X1008-0-0-47 14X1008-0-0-48 14X1008-0-0-49 14X1008-0-0-5 14X1008-0-0-50 14X1008-0-0-54 14X1008-0-0-6 14X1008-0-0-61 14X1008-0-0-65 14X1008-0-0-7 14X1008-0-0-77 14X1008-0-0-78 14X1008-0-0-8 14X1008-0-0-82 14X1008-0-0-83 14X1008-0-0-85 14X1008-0-0-9 14X1022-0-0-12 14X1022-0-0-16 14X1022-0-0-2 14X1022-0-0-39 14X1022-0-0-43 14X1022-0-0-46 14X1022-0-0-49 14X1022-0-0-52 14X1022-0-0-53 14X1022-0-0-56 14X1022-0-0-59 14X1022-0-0-60 14X1022-0-0-61 14X1022-0-0-64 14X1022-0-0-66 14X1022-0-0-68 14X1022-0-0-70 14X1022-0-0-72 14X1022-0-0-76 14X1022-0-0-78 14X1023-0-0-18 14X1023-0-0-30 14X1023-0-0-33 14X1023-0-0-38 14X1023-0-0-39 14X1023-0-0-4 14X1023-0-0-45 14X1023-0-0-48 14X1023-0-0-49 14X1023-0-0-59 14X1023-0-0-70 14X1023-0-0-71 14X1023-0-0-73 14X1023-0-0-74 14X1023-0-0-75 14X1023-0-0-76 14X1023-0-0-78 14X1023-0-0-79 14X1023-0-0-80 14X1023-0-0-82 14X1023-0-0-85 14X1023-0-0-89 14X1023-0-0-90 14X1023-0-0-91 14X1027-0-0-104 14X1027-0-0-107 14X1027-0-0-11 14X1027-0-0-110 14X1027-0-0-112 14X1027-0-0-117 14X1027-0-0-121 14X1027-0-0-122 14X1027-0-0-123 14X1027-0-0-126 14X1027-0-0-128 14X1027-0-0-17 14X1027-0-0-22 14X1027-0-0-23 14X1027-0-0-25 14X1027-0-0-36 14X1027-0-0-37 14X1027-0-0-39 14X1027-0-0-4 14X1027-0-0-40 14X1027-0-0-43 14X1027-0-0-44 14X1027-0-0-45 14X1027-0-0-59 14X1027-0-0-62 14X1027-0-0-70 14X1027-0-0-77 14X1027-0-0-8 14X1027-0-0-82 14X1027-0-0-85 14X1027-0-0-92 14X1027-0-0-94 14X1030-0-0-1 14X1030-0-0-111 14X1030-0-0-112 14X1030-0-0-113 14X1030-0-0-120 14X1030-0-0-123 14X1030-0-0-128 14X1030-0-0-13 14X1030-0-0-131 14X1030-0-0-135 14X1030-0-0-14 14X1030-0-0-141 14X1030-0-0-145 14X1030-0-0-149 14X1030-0-0-16 14X1030-0-0-160 14X1030-0-0-161 14X1030-0-0-164 14X1030-0-0-168 14X1030-0-0-17 14X1030-0-0-176 14X1030-0-0-177 14X1030-0-0-18 14X1030-0-0-185 14X1030-0-0-188 14X1030-0-0-2 14X1030-0-0-215 14X1030-0-0-216 14X1030-0-0-220 14X1030-0-0-222 14X1030-0-0-226 14X1030-0-0-228 14X1030-0-0-25 14X1030-0-0-29 14X1030-0-0-36 14X1030-0-0-40 14X1030-0-0-54 14X1030-0-0-55 14X1030-0-0-68 14X1030-0-0-71 14X1030-0-0-72 14X1030-0-0-76 14X1030-0-0-77 14X1030-0-0-78 14X1030-0-0-80 14X1030-0-0-81 14X1030-0-0-84 14X1030-0-0-88 14X1030-0-0-93 14X1030-0-0-97 14X1031-0-0-105 14X1031-0-0-110 14X1031-0-0-112 14X1031-0-0-113 14X1031-0-0-114 14X1031-0-0-117 14X1031-0-0-120 14X1031-0-0-121 14X1031-0-0-125 14X1031-0-0-134 14X1031-0-0-136 14X1031-0-0-14 14X1031-0-0-141 14X1031-0-0-143 14X1031-0-0-147 14X1031-0-0-149 14X1031-0-0-16 14X1031-0-0-160 14X1031-0-0-161 14X1031-0-0-18 14X1031-0-0-2 14X1031-0-0-20 14X1031-0-0-21 14X1031-0-0-22 14X1031-0-0-23 14X1031-0-0-24 14X1031-0-0-28 14X1031-0-0-29 14X1031-0-0-3 14X1031-0-0-30 14X1031-0-0-32 14X1031-0-0-34 14X1031-0-0-35 14X1031-0-0-36 14X1031-0-0-4 14X1031-0-0-51 14X1031-0-0-52 14X1031-0-0-59 14X1031-0-0-6 14X1031-0-0-60 14X1031-0-0-64 14X1031-0-0-90 14X1031-0-0-93 14X1031-0-0-94 14X1031-0-0-96 14X1053-0-0-10 14X1053-0-0-103 14X1053-0-0-106 14X1053-0-0-107 14X1053-0-0-109 14X1053-0-0-110 14X1053-0-0-111 14X1053-0-0-118 14X1053-0-0-120 14X1053-0-0-124 14X1053-0-0-128 14X1053-0-0-13 14X1053-0-0-130 14X1053-0-0-131 14X1053-0-0-132 14X1053-0-0-133 14X1053-0-0-136 14X1053-0-0-137 14X1053-0-0-138 14X1053-0-0-139 14X1053-0-0-14 14X1053-0-0-142 14X1053-0-0-143 14X1053-0-0-146 14X1053-0-0-147 14X1053-0-0-149 14X1053-0-0-15 14X1053-0-0-151 14X1053-0-0-153 14X1053-0-0-154 14X1053-0-0-155 14X1053-0-0-157 14X1053-0-0-158 14X1053-0-0-162 14X1053-0-0-164 14X1053-0-0-166 14X1053-0-0-167 14X1053-0-0-168 14X1053-0-0-169 14X1053-0-0-170 14X1053-0-0-172 14X1053-0-0-174 14X1053-0-0-179 14X1053-0-0-180 14X1053-0-0-182 14X1053-0-0-19 14X1053-0-0-20 14X1053-0-0-23 14X1053-0-0-28 14X1053-0-0-29 14X1053-0-0-31 14X1053-0-0-33 14X1053-0-0-37 14X1053-0-0-4 14X1053-0-0-47 14X1053-0-0-5 14X1053-0-0-51 14X1053-0-0-52 14X1053-0-0-54 14X1053-0-0-55 14X1053-0-0-56 14X1053-0-0-58 14X1053-0-0-59 14X1053-0-0-6 14X1053-0-0-61 14X1053-0-0-63 14X1053-0-0-65 14X1053-0-0-66 14X1053-0-0-7 14X1053-0-0-71 14X1053-0-0-73 14X1053-0-0-74 14X1053-0-0-75 14X1053-0-0-76 14X1053-0-0-77 14X1053-0-0-78 14X1053-0-0-80 14X1053-0-0-81 14X1053-0-0-82 14X1053-0-0-87 14X1053-0-0-89 14X1053-0-0-9 14X1053-0-0-91 14X1053-0-0-92 14X1053-0-0-93 14X1053-0-0-97 14X1053-0-0-98 14X1054-0-0-1 14X1054-0-0-10 14X1054-0-0-14 14X1054-0-0-18 14X1054-0-0-2 14X1054-0-0-27 14X1054-0-0-28 14X1054-0-0-3 14X1054-0-0-31 14X1054-0-0-32 14X1054-0-0-34 14X1054-0-0-46 14X1054-0-0-5 14X1054-0-0-55 14X1054-0-0-6 14X1054-0-0-60 14X1054-0-0-61 14X1054-0-0-62 14X1054-0-0-64 14X1054-0-0-65 14X1054-0-0-9 14X1082-0-0-10 14X1082-0-0-12 14X1082-0-0-19 14X1082-0-0-20 14X1082-0-0-21 14X1082-0-0-22 14X1082-0-0-25 14X1082-0-0-27 14X1082-0-0-34 14X1082-0-0-7 14X1083-0-0-10 14X1083-0-0-100 14X1083-0-0-103 14X1083-0-0-104 14X1083-0-0-108 14X1083-0-0-112 14X1083-0-0-118 14X1083-0-0-12 14X1083-0-0-120 14X1083-0-0-129 14X1083-0-0-130 14X1083-0-0-134 14X1083-0-0-14 14X1083-0-0-140 14X1083-0-0-142 14X1083-0-0-146 14X1083-0-0-15 14X1083-0-0-157 14X1083-0-0-161 14X1083-0-0-162 14X1083-0-0-166 14X1083-0-0-167 14X1083-0-0-168 14X1083-0-0-174 14X1083-0-0-18 14X1083-0-0-183 14X1083-0-0-188 14X1083-0-0-191 14X1083-0-0-192 14X1083-0-0-197 14X1083-0-0-205 14X1083-0-0-213 14X1083-0-0-218 14X1083-0-0-221 14X1083-0-0-223 14X1083-0-0-230 14X1083-0-0-231 14X1083-0-0-234 14X1083-0-0-235 14X1083-0-0-238 14X1083-0-0-24 14X1083-0-0-243 14X1083-0-0-245 14X1083-0-0-251 14X1083-0-0-254 14X1083-0-0-256 14X1083-0-0-26 14X1083-0-0-260 14X1083-0-0-268 14X1083-0-0-3 14X1083-0-0-30 14X1083-0-0-33 14X1083-0-0-4 14X1083-0-0-46 14X1083-0-0-54 14X1083-0-0-59 14X1083-0-0-63 14X1083-0-0-65 14X1083-0-0-67 14X1083-0-0-71 14X1083-0-0-72 14X1083-0-0-76 14X1083-0-0-8 14X1083-0-0-86 14X1083-0-0-88 14X1083-0-0-9 14X1083-0-0-91 14X1083-0-0-93 14X1083-0-0-96 14X1083-0-0-99 14X1085-0-0-10 14X1085-0-0-11 14X1085-0-0-27 14X1085-0-0-34 14X1085-0-0-36 14X1085-0-0-56 14X1085-0-0-58 14X1085-0-0-59 14X1085-0-0-68 14X1085-0-0-71 14X1085-0-0-8 14X1085-0-0-83 14X1085-0-0-90 14X1085-0-0-93 14X1085-0-0-96 14X1098-0-0-10 14X1098-0-0-106 14X1098-0-0-109 14X1098-0-0-18 14X1098-0-0-30 14X1098-0-0-31 14X1098-0-0-34 14X1098-0-0-38 14X1098-0-0-39 14X1098-0-0-4 14X1098-0-0-41 14X1098-0-0-46 14X1098-0-0-48 14X1098-0-0-53 14X1098-0-0-54 14X1098-0-0-57 14X1098-0-0-7 14X1098-0-0-70 14X1098-0-0-72 14X1098-0-0-73 14X1098-0-0-79 14X1098-0-0-8 14X1098-0-0-81 14X1098-0-0-83 14X1098-0-0-94 14X1098-0-0-95 14X1098-0-0-96 14X1098-0-0-98 14X1103-0-0-104 14X1103-0-0-105 14X1103-0-0-106 14X1103-0-0-114 14X1103-0-0-115 14X1103-0-0-116 14X1103-0-0-117 14X1103-0-0-12 14X1103-0-0-120 14X1103-0-0-122 14X1103-0-0-124 14X1103-0-0-130 14X1103-0-0-131 14X1103-0-0-135 14X1103-0-0-136 14X1103-0-0-138 14X1103-0-0-141 14X1103-0-0-143 14X1103-0-0-146 14X1103-0-0-147 14X1103-0-0-148 14X1103-0-0-150 14X1103-0-0-155 14X1103-0-0-157 14X1103-0-0-159 14X1103-0-0-16 14X1103-0-0-162 14X1103-0-0-18 14X1103-0-0-27 14X1103-0-0-3 14X1103-0-0-31 14X1103-0-0-33 14X1103-0-0-37 14X1103-0-0-41 14X1103-0-0-42 14X1103-0-0-50 14X1103-0-0-51 14X1103-0-0-56 14X1103-0-0-58 14X1103-0-0-6 14X1103-0-0-63 14X1103-0-0-64 14X1103-0-0-68 14X1103-0-0-75 14X1103-0-0-76 14X1103-0-0-77 14X1103-0-0-79 14X1103-0-0-8 14X1103-0-0-80 14X1103-0-0-81 14X1103-0-0-83 14X1103-0-0-91 14X1103-0-0-96 14X1114-0-0-1 14X1114-0-0-101 14X1114-0-0-104 14X1114-0-0-105 14X1114-0-0-18 14X1114-0-0-23 14X1114-0-0-25 14X1114-0-0-26 14X1114-0-0-32 14X1114-0-0-36 14X1114-0-0-37 14X1114-0-0-4 14X1114-0-0-45 14X1114-0-0-48 14X1114-0-0-54 14X1114-0-0-60 14X1114-0-0-62 14X1114-0-0-64 14X1114-0-0-7 14X1114-0-0-73 14X1114-0-0-75 14X1114-0-0-79 14X1114-0-0-80 14X1114-0-0-84 14X1114-0-0-85 14X1114-0-0-90 14X1114-0-0-91 14X1114-0-0-92 14X1114-0-0-93 14X1114-0-0-97 14X1115-0-0-11 14X1115-0-0-14 14X1115-0-0-17 14X1115-0-0-2 14X1115-0-0-20 14X1115-0-0-21 14X1115-0-0-22 14X1115-0-0-25 14X1115-0-0-26 14X1115-0-0-28 14X1115-0-0-29 14X1115-0-0-31 14X1115-0-0-37 14X1115-0-0-41 14X1115-0-0-45 14X1115-0-0-48 14X1115-0-0-49 14X1115-0-0-5 14X1115-0-0-50 14X1115-0-0-51 14X1115-0-0-52 14X1115-0-0-53 14X1115-0-0-55 14X1115-0-0-56 14X1115-0-0-58 14X1115-0-0-6 14X1115-0-0-60 14X1115-0-0-62 14X1115-0-0-64 14X1115-0-0-66 14X1115-0-0-68 14X1115-0-0-69 14X1115-0-0-7 14X1115-0-0-73 14X1115-0-0-74 14X1115-0-0-77 14X1117-0-0-104 14X1117-0-0-114 14X1117-0-0-117 14X1117-0-0-12 14X1117-0-0-14 14X1117-0-0-23 14X1117-0-0-24 14X1117-0-0-26 14X1117-0-0-29 14X1117-0-0-3 14X1117-0-0-35 14X1117-0-0-36 14X1117-0-0-37 14X1117-0-0-38 14X1117-0-0-4 14X1117-0-0-43 14X1117-0-0-45 14X1117-0-0-46 14X1117-0-0-49 14X1117-0-0-50 14X1117-0-0-55 14X1117-0-0-6 14X1117-0-0-61 14X1117-0-0-64 14X1117-0-0-67 14X1117-0-0-69 14X1117-0-0-70 14X1117-0-0-72 14X1117-0-0-73 14X1117-0-0-74 14X1117-0-0-79 14X1117-0-0-8 14X1117-0-0-82 14X1117-0-0-83 14X1117-0-0-84 14X1117-0-0-85 14X1117-0-0-89 14X1117-0-0-9 14X1117-0-0-90 14X1117-0-0-92 14X1117-0-0-94 14X1117-0-0-96 14X1117-0-0-98 14X1117-0-0-99 14X1118-0-0-11 14X1118-0-0-119 14X1118-0-0-139 14X1118-0-0-14 14X1118-0-0-142 14X1118-0-0-15 14X1118-0-0-17 14X1118-0-0-173 14X1118-0-0-174 14X1118-0-0-178 14X1118-0-0-18 14X1118-0-0-188 14X1118-0-0-190 14X1118-0-0-194 14X1118-0-0-196 14X1118-0-0-198 14X1118-0-0-199 14X1118-0-0-20 14X1118-0-0-204 14X1118-0-0-208 14X1118-0-0-21 14X1118-0-0-22 14X1118-0-0-226 14X1118-0-0-23 14X1118-0-0-24 14X1118-0-0-26 14X1118-0-0-28 14X1118-0-0-32 14X1118-0-0-34 14X1118-0-0-35 14X1118-0-0-36 14X1118-0-0-37 14X1118-0-0-42 14X1118-0-0-43 14X1118-0-0-48 14X1118-0-0-50 14X1118-0-0-51 14X1118-0-0-52 14X1118-0-0-6 14X1118-0-0-64 14X1118-0-0-72 14X1118-0-0-92 14X1118-0-0-95 14X1118-0-0-99 ARS Crescent BRUEHL Bobtail Jasper LCS-HULK Otto Pritchett SY Banks SY Command |
| d2 | 2 | 1 2 |
| Dimensions | |
|---|---|
| Covariance Parameters | 3 |
| Columns in X | 925 |
| Columns in Z | 0 |
| Subjects | 1 |
| Max Obs per Subject | 1151 |
| Number of Observations | |
|---|---|
| Number of Observations Read | 1151 |
| Number of Observations Used | 1151 |
| Number of Observations Not Used | 0 |
| Parameter Search | |||||
|---|---|---|---|---|---|
| CovP1 | CovP2 | CovP3 | Variance | Res Log Like | -2 Res Log Like |
| 0.07400 | 0.005100 | 0.4750 | 0.07973 | -65.8701 | 131.7401 |
| Iteration History | |||
|---|---|---|---|
| Iteration | Evaluations | -2 Res Log Like | Criterion |
| 1 | 1 | 131.74010908 | 0.00000000 |
| Convergence criteria met but final Hessian is not positive definite. |
| Covariance Parameter Estimates | ||
|---|---|---|
| Cov Parm | Subject | Estimate |
| Variance | Intercept | 0.01242 |
| SP(POW) | Intercept | 0.005100 |
| Residual | 0.07973 | |
| Fit Statistics | |
|---|---|
| -2 Res Log Likelihood | 131.7 |
| AIC (Smaller is Better) | 137.7 |
| AICC (Smaller is Better) | 137.8 |
| BIC (Smaller is Better) | 148.0 |
| PARMS Model Likelihood Ratio Test | ||
|---|---|---|
| DF | Chi-Square | Pr > ChiSq |
| 2 | 0.00 | 1.0000 |
| Type 3 Tests of Fixed Effects | ||||
|---|---|---|---|---|
| Effect | Num DF | Den DF | F Value | Pr > F |
| d2 | 1 | 229 | 38.04 | <.0001 |
| name(d2) | 920 | 229 | 1.38 | 0.0016 |
| Least Squares Means | ||||||
|---|---|---|---|---|---|---|
| Effect | d2 | Estimate |
Standard Error |
DF | t Value | Pr > |t| |
| d2 | 1 | 2.2005 | 0.02276 | 229 | 96.68 | <.0001 |
| d2 | 2 | 2.0471 | 0.01005 | 229 | 203.77 | <.0001 |